I. Introduction                                                                                    

II. Les Principes de la Méthode D’Elliott                             

A. L’apport de Fibonacci                                                             

1. La séquence de Fibonacci                                                       

2. Le « Nombre d’Or » et le « Ratio d’Or »                            

3. La « Spirale Logarithmique »                                              

 

B. Les règles de base                                                                  

1. Introduction et terminologie                                          

a) Introduction                                                                                   

b) Terminologie                                                                                 

2. Les règles impératives                                                          

a) Le principe                                                                                     

b) Les règles de base                                                                          

3. La durée : une nouvelle classification.                        

a) à propos des degrés ...                                                                   

b) Application                                                                                    

c) Exemple                                                                                        

III. Les configurations                                                                  

1. Les figures de correction                                                   

a) Le Zig-Zag (5-4-5)                                                                          

b) Le Flat                                                                                           

c) La Poussée                                                                                    

d) Les Triangles                                                                                 

2. Les figures d’impulsion                                                         

a) L’Impulsion Standard                                                                     

b) L’extension                                                                                   

c) La Cassure                                                                                    

d) Le Triangle Diagonal                                                                      

IV. Une Nouvelle Approche De La Méthode D’Elliott : L’Utilisation De L’Indicateur De Saturation                                                 

A. Introduction                                                                             

1. Principes de base des oscillateurs                                 

2. Les principaux signaux fournis par les oscillateurs

 

B. Présentation du modèle M.A.C.D. (Moving Average Convergence Divergence)                                                      

1. Définition                                                                                    

2. Construction                                                                            

3. Avantages du modèle M.A.C.D.                                            

4. Inconvénient du modèle M.A.C.D.                                       

5. Application du modèle M.A.C.D.                                          

6. Conclusion                                                                                 

 

C. Présentation du Stochastique                                       

1. Définition                                                                                    

2. Construction                                                                            

3. Avantage du stochastique                                                 

4. Inconvénient du stochastique                                          

 

D. L’Indicateur de Saturation                                               

 

E. L’apport de L’Indicateur de Saturation pour la méthode d’Elliott                                                                                           

IV. Conclusion                                                                                     73

 

I.          Introduction

 

 

 

Depuis quelques années, dans la littérature financière, on assiste à de nombreux débats concernant l’utilisation croissante de nouveaux outils d’analyse et de prévision des mouvements de marché. Ces outils faisant appel à une étude de l’évolution d’un marché, principalement sur la base d’études graphiques sont englobés sous le terme d’analyse technique, selon la définition de John J. Murphy (1986).

 

Ces pratiques sont souvent opposées à l’analyse fondamentale.

 

· Les analystes fondamentaux pensent qu’il faut chercher dans certaines informations, certains indicateurs économiques (les fondamentaux, à déterminer suivant les variables étudiées), les orientations futures des mouvements de marchés.

· Pour les analystes techniques, le marché est irrationnel : les marchés financiers sont épidermiques et leur psychologie n’a rien à voir avec la logique que fournit l’analyse fondamentale. Ils ne sont pas régis par la raison, mais par la psychologie des foules.

 

Faut-il être chartiste, fondamentaliste ou défenseur de l’efficience des marchés, adopter des règles systématiques de trading, ou tout simplement se fier à son intuition, au « bon sens » ou aux « rumeurs », comme le font bon nombre de traders ?

 

Bien évidemment, et on peut le regretter, il n’y a pas de réponse nette : tout va dépendre de l’état du marché, de l’horizon temporel de prévision et des objectifs que l’on se fixe.

 

Par ailleurs, il faut éviter d’opposer systématiquement analyse fondamentale et analyse technique. Non seulement ce débat n’apporte rien, mais en plus, il ne semble pas avoir de sens réel. Les deux approches sont complémentaires et l’état du marché ainsi que l’horizon temporel de la prévision « dicte » la méthode à employer.

 

 

Aussi, de nombreuses études qui ont tenté de monter le pouvoir prédictif des modèles fondamentaux ont abouti aux conclusions suivantes :

 

Ä En premier lieu, plus l’horizon temporel est court et plus la marche au hasard (« Random Walk ») semble de nature à donner de meilleurs résultats que les modèles, selon les critères choisis (R. Meese et K. Rogoff (1983,1984), M. Finn (1986)) ;

 

Ä Par ailleurs, ces modèles semblent plus appropriés pour prévoir l’évolution des cours au-delà d’un mois (R. Meese et K. Rogoff (1983,1984), M. Finn (1986)) ;

 

Ces remarques illustrent bien la réelle difficulté que rencontrent les modèles fondamentaux et la faiblesse de leur pouvoir prédictif surtout dans le très court terme.

 

En effet, ces résultats ont sérieusement remis en question l’hypothèse d’efficience au sens fort des marchés (par opposition à l’efficience globale, sur le très long terme). Et cela d’autant plus que les analystes se sont rendu compte que les marchés ne mouvaient plus s’analyser d’un point de vue macro-économique et qu’il était nécessaire de les considérer comme un enchevêtrement de microstructures, intégrant de nouvelles propriétés comme les anticipations, les comportements mimétiques, la notion de risque systémique, etc....

 

Mais malgré ces échecs, il est évident que les acteurs sur les marchés sont dans l’obligation de s’intéresser à la formation des cours à très court terme (« intra-days »); d’où le développement de nouveaux outils de prévision faisant appel à l’analyse technique.

 

En particulier, dans la littérature comme sur les marchés, la méthode de prévision issue des travaux d’Elliott est considérée comme la plus aboutie des analyses techniques dans le domaine chartiste, celle qui donne les meilleurs résultats et par conséquent la plus appliquée.

 

En effet, Elliott a donné une dimension nouvelle aux travaux chartistes de son prédécesseur Charles Dow, notamment à travers le concept de vagues, plus connue sous l’appellation « Elliott Waves ».

 

C’est la raison pour laquelle il nous a semblé intéressant de présenter et, par la même occasion démystifier la théorie des Vagues d’Elliott, car elle est la plus répandue actuellement et donc exerce une forte influence sur les marchés� .

 

Ainsi il sera intéressant de présenter dans un premier temps les principes de la méthode d’Elliott, en traitant successivement de l’apport des travaux de L. Fibonacci et des règles de base de cette méthode d’analyse technique.

Puis dans une seconde partie, nous présenterons un développement récent des modalité d’application de la méthode, réduisant le risque d’erreur et palliant à certaines limites: il s’agit de l’utilisation de l’indicateur de saturation.

 

 

 

 

II.          Les Principes de la Méthode D’Elliott

 

La théorie des Vagues d’Elliott est essentiellement un système de règles empiriques visant l’interprétation de l’évolution  des cours sur les marchés financier afin d’effectuer des prévisions.

Cette méthode est perçue comme étant la plus complète et la mieux élaborée. En effet, le principal avantage de cette méthode est qu’elle se caractérise par sa généralité et sa précision. La généralité donne très souvent du recul par rapport au marché et la précision permet de déceler les changements de direction. Par ailleurs, elle repose sur une vision psychologique des marchés.

La théorie d’Elliott est également la théorie la plus travaillée et la plus suivie. Elle offre l’avantage d’intégrer certains éléments de l’analyse chartiste traditionnelle. Pour cela, elle peut être considérée comme une théorie enveloppante de l’analyse technique.

 

Après avoir décrit l’apport de L. Fibonacci, nous présenterons les règles qui régissent cette méthode, ainsi que les modifications subies récemment par celle-ci.

 

A.          L’apport de Fibonacci 

 

Les travaux de R.N. Elliott connurent deux influences bien différentes. Tout d’abord, il approfondit certains principes que Charles Dow n’avait qu’esquissés. Chez les deux hommes, la psychologie humaine est aussi déterminante pour comprendre l’évolution des marchés (mais Elliott va plus loin dans son analyse). Une des preuves irréfutables de cette influence se retrouve d’ailleurs dans les termes qu’Elliott emploie et qui font référence à la mer (notamment le terme de « vague »).

 

Le second guide d’Elliott est beaucoup plus inattendu et plus éloigné dans le temps puisqu’il s’agît de Leonardo Fibonacci, mathématicien du XIII^e siècle, auquel R.N. Elliott va reprendre une partie de ses conclusions concernant le Nombre d’Or et la fameuse série de Fibonacci.

 

L’intuition d’Elliott est assez étonnante: il suppose, en effet, que les fluctuations des marchés sont le reflet d’une somme de réactions psychologiques individuelles (Dow) et doivent refléter une harmonie fondamentale de la nature (Fibonacci).

 

Selon lui, les marchés doivent fluctuer en respectant une harmonie naturelle, telle qu’on peut la retrouver dans la plupart des manifestations découvertes par Fibonacci. Les marchés doivent ainsi varier en suivant une certaine perfection ordonnée par la nature et qui est celle découverte par Fibonacci.

 

A partir de la série mathématique et des ratios de Fibonacci et après une étude pointilleuse de l’évolution du Dow Jones, R.N. Elliott est parvenu à déduire un ensemble de principes et de règles qui fondent sa théorie. Nous les exposerons plus loin.

 

Donc, dans son dernier ouvrage sur le principe des vagues Nature’s Law - The secret of the Universe , Elliott lui-même considérait que la base de la théorie des vagues est une suite de nombres, ou plus exactement une séquence mathématique découverte par ce mathématicien du XIII^e: Leonardo Fibonacci.

 

 

Né  à Pise entre 1170 et 1180, Leonardo Fibonacci, dont le père était un officier de l’administration et un commerçant renommé, fût le premier mathématicien à introduire le système décimal et les chiffres arabes (0, 1, 2, 3, 4, 5, 6, 7, 8 et 9) en Europe, grâce à son ouvrage Liber Abaci (Livre de Calcul) publié en 1202 puis revu en 1228. Ce système de chiffres devenu universel avait le mérite d’offrir une puissance de calcul incomparable à celle des systèmes numériques grecs et romains qui utilisaient les sept symboles I, V, X, L, D et M. Il introduisait également le 0 jusqu’alors inconnu.

 

Fibonacci fût un des plus grands mathématiciens du moyen âge et posa les jalons d’importants développements en mathématiques, en physique et en astronomie. Il publia ainsi deux autres oeuvres Practicia Geometriae et Liber Quadratorum, mais malgré l’apport considérable de ses travaux, l’homme est resté dans l’oubli.

 

 

1.  La séquence de Fibonacci

 

 

Dans l’ouvrage Liber Abaci, Fibonacci présente une série de nombres aux pouvoirs multiples, que l’on appelle la séquence de Fibonacci. La série est la suivante:

 

 

 

 

Elle se construit  de façon très simple : on obtient chaque chiffre en sommant les deux derniers chiffres de la série.

 

 

L’auteur présente d’abord sa découverte comme la solution à un problème mathématique concernant le taux de reproduction des lapins. En effet, le problème posé était:

 

« Un couple de lapins étant dans un espace clos, combien de couples de lapins peut-il engendrer en un an sachant que chaque couple donne naissance à un nouveau couple  à partir du deuxième mois ? »

 

 

La figure 1 montre l’arbre généalogique de la famille de lapins dont la croissance est exponentielle.

 

 

Mois			arbre généalogique des lapins																		Couples
1																							1
2																							1
3																							2
4																							3
5																							5
6																							8
7																							13
8																							21
En 12 mois M. et Mme Lapin auront une famille de 144 couples
12																							144

 

figure 1

 

 

 

La séquence de Fibonacci résultant du problème des lapins possède beaucoup de propriétés intéressantes; les nombres qui la composent étant entre autres liés par une relation constante. Nous ne présenterons que les quatre propriétés les plus intéressantes, car les autres n’ont qu’un rapport lointain avec le sujet nous concernant, à savoir la méthode d’Elliott.

 

 

Voici ces propriétés:

 

 

Œ La somme de deux nombres adjacents quelconques de la séquence donne le nombre suivant de la séquence:

 

 

 

 

 

 

Par exemple :     1 + 1 = 2              8 + 13 = 21

                          1 + 2 = 3              13 + 21 = 34

                          2 + 3 = 5              21 + 34 = 55

                          3 + 5 = 8              34 + 55 = 89

                          5 + 8 = 13             etc ... jusqu’à n ® ¥

 

 

Le détail des prochaines propriétés peut être observé sur la Fig. 2 qui est une table des ratios entre tous les nombres de Fibonacci de 1 à 44

 

 

figure 2

 

 

 

� Plus on va loin dans la série, plus le rapport de deux nombres consécutifs approche 1,618 (Nombre d’Or) ou son inverse 0,618(Ratio d’Or) et ceci à partir du quatrième nombre de la séquence.

 

 

 

 

 

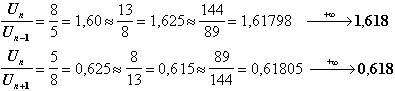
Ž Le rapport de deux nombres pris un sur deux dans la séquence est 2,618 ou son inverse 0,382

 

 

 

 

 

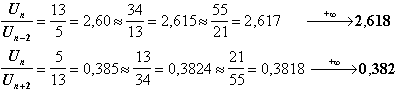
� La série de Fibonacci dispose de bien d’autres propriétés, mais le plus important réside dans celles, beaucoup plus troublantes, du « Nombre d’Or » et du « Ratio d’Or » (1, 618 et 0,618)

 

2.  Le « Nombre d’Or » et le « Ratio d’Or »

 

 

Ils peuvent être calculé précisément de la manière suivante :

 

 

 

Les proportions qu’ils représentent sont plaisantes à l’oeil. On les rencontre souvent dans la musique, les arts, l’architecture et la biologie. William Hoffer écrivait ainsi dans le Smithsonian Magazine de décembre 1975 :

 

«  ...... le rapport de 0,618034 à 1 est la base mathématique de la forme des cartes à jouer, du Parthénon, des tournesols, des coquilles d’escargot, des vases grecs et des galaxies lointaines en spirale. Les grecs utilisaient beaucoup cette proportion dans leur art et leur architecture. Ils l’appelaient déjà le Nombre d’Or.  [...]  Les apparitions répétées‚ des nombres de Fibonacci et de la Spirale d’Or dans la nature explique exactement pourquoi la proportion de 0,618034 à 1 est si agréable dans l’art. L’homme perçoit ainsi l’image de la vie dans l’art à travers le Nombre d’Or. »

 

 

De même, la confrérie pythagoricienne avait choisi l’étoile à cinq branches comme symbole, chaque segment étant relié au segment inférieur suivant le Nombre d’Or. L’Egypte antique avait déjà adopté à jamais le Nombre d’Or, à travers la construction des pyramides dont l’hypoténuse a une longueur égale à 161,8% de la moitié de la base, de telle sorte que la hauteur de la pyramide est la racine carrée de 161,8% de la moitié de la base.

 

Aussi, R.N. Elliott a été le premier à observer que les marchés évoluaient aussi en suivant un certain ordre, régit par la séquence de Fibonacci.

 

Il a donc mis en relation les enseignements de son prédécesseur Charles Dow, selon lesquels le marché et le prix du marché ne sont que la représentation de l’ensemble de ses intervenants et de leur psychologie, et ceux de Fibonacci selon lesquels l’univers est régit par un ordre. En effet, selon R. Prechter, « il ne faut pas rejeter la possibilité pour le marché des actions d’avoir aussi une forme; car il est aussi une partie de la réalité de la vie ». R.N. Elliott va même au delà de toutes les autres théories dans l’étude de la forme, il stipule que « quels que soient l’horizon de temps et la forme, le schéma de base reste le même ».

 

L’évolution des marchés peut être comparée à la forme d’une Spirale Logarithmique.

 

 

3.  La « Spirale Logarithmique »

 

 

La première étape de sa construction est l’élaboration d’un Rectangle d’Or, lequel est divisé ensuite en un carré et un plus petit Rectangle d’Or, comme sur la figure 3. Ce processus peut théoriquement être répété à l’infini. Il apparaît que les carré en résultant, marqués A, B, C, D, E, F, etc... s’enroulent vers le centre.

Les diagonales en pointillé, elles-mêmes liées par le Nombre d’Or, soulignent le centre théorique des carrés qui s’enroulent.

 

Une spirale peut être tracée à partir de ce point central, en reliant les points d’intersection avec chaque carré par ordre de taille grandissante. Ces points tracent une Spirale Logarithmique.

 

 

 

 

figure 3

 

 

La Spirale Logarithmique est, comme les Vagues d’Elliott, sans limite et garde une forme constante. Si l’on regarde une Spirale Logarithmique à travers un microscope, l’allure générale est la même que celle de la spirale d’une galaxie vue à travers un télescope .

 

Un seconde propriété de cette spirale est que, où que l’on soit dans la spirale logarithmique, le ratio entre tout rayon à partir du centre théorique de la spirale et celui qui le précède à 90 degrés, est égal à 1,618 (fig. 4); Nous verrons que dans la théorie d’Elliott ce phénomène est observé lorsque l’on évolue d’un degré à un autre.

 

figure 4

 

 

 

 

Les nombres de Fibonacci ont encore bien d’autres propriétés, mais celles que nous venons de détailler suffisent déjà pour apprécier l’importance de ces nombres tant dans notre vie de tous les jours que dans l’univers le plus lointain.

 

La question qui se pose est : « Tout cela a-t-il vraiment quelque chose à voir avec les marché financiers ? »

 

Pour Elliott, la réponse est affirmative; Inspiré par cette omniprésence universelle du Nombre d’Or et des autres ratios de la série, Elliott en a conclu que les cours de la bourse devaient également être entretenus par ce véritable mystère de la nature. En effet, l’auteur considère que « le concept idéal de progression d’un marché est une base excellente pour la construction de la Spirale d’Or », comme illustré sur la figure 5 toutefois très approximative. Dans cette construction, le sommet de chaque vague successive de degré supérieur touche la courbe en expansion logarithmique, ce qui laisse entrevoir d’importantes propriétés sur ces vagues.

 

 

 

 

 

 

figure 5

 

 

Selon A.J. Frost ce principe apparaît si clairement dans les marchés financiers car ces marchés sont la plus importante manifestation de psychologie de masse au monde, « un reflet presque parfait de la condition psychologique collective de l’humanité, tout en étant lié à la réalité de l’évolution de l’homme, à l’économie et au monde des affaires. »

 

 

Le marché financier aurait bien la même base mathématique que tous ces phénomènes naturels. Il restait « simplement » à en découvrir la formule et les règles. Elliott y consacra en tout près de vingt ans de sa vie et nous à légué une véritable théorie pratique de l’influence des Nombres de Fibonacci sur l’évolution des marchés financiers, tout en conservant une vision pragmatique basée sur la psychologie des intervenants.

 

 

Nous allons maintenant consacrer la prochaine partie à la présentation des règles de base de la théorie d’Elliott, en y apportant la vision la plus actualisée possible.

 

B.          Les règles de base

 

1.  Introduction et terminologie

a) Introduction

 

Avant d’aborder la méthode d’Elliott, nous allons justifier le choix de cet outil, en expliquant à quels problèmes sont confrontés les analystes avec les marchés d’une part, avec les autres outils d’analyse d’autre part.

 

Pour prendre des décisions avec un maximum de sécuritéƒ , l’approche doit s’effectuer selon trois directions :

 

Ä une analyse historique qui permet de connaître l’évolution des cours, volumes et positions ouvertes sur la durée la plus longue possible.

Ä une analyse en terme de temps et d’amplitude.

Ä utiliser les modèles les plus efficients.

 

· En effet, l’analyste technique prend pour hypothèses que le marché à de la mémoire, que le prix du marché contient toute l’information disponible (le marché est efficient) et que l’histoire se répète. Par conséquent pour réaliser des prévisions à l’aide de l’analyse technique, il faut disposer de graphiques complets quelque soit l’horizon de la prévision. Les spécialistes des valeurs françaises connaissent bien l’indice INSEE base 100 1949, référence incontournable du marché parisien.

Ces graphiques doivent être disponibles sur des bases mensuelles, hebdomadaires, quotidiennes, horaires et sub-horaires correspondant aux différents niveaux de l’indicateur de. A l’heure actuelle, tous les bons logiciels permettent cette subdivision.

 

· En ce qui concerne la question de temps et d’amplitude, bien souvent les opérateurs ne s’intéressent qu’aux variations de cours ou bien d’indices ( la plupart des modèles d’analyse technique donnent des signaux qualitatifs). Bien que ce paramètre soit essentiel pour réaliser une stratégie, il est évident que la notion de temps le soit autant sinon plus. En effet, un opérateur aura souvent une bonne prévision en amplitude, mais il perdra de l’argent s’il ne sait pas à quel moment il devra dénouer sa position. Cet problème parait bénin, mais il devient crucial lorsque l’opérateur se situe sur un marché de contrats à terme où il faut payer des marges journalières lorsque les cours évoluent à l’inverse de celui escompté.

 

· En ce qui concerne l’utilisation des modèles, il semble opportun  d’estimer des résultats et de les confirmer par un ou plusieurs modèles. En effet, la décision se fera lorsque les prévisions seront concordantes sur plusieurs modèles„ . Aussi, on diminue le degré d’incertitude lors d’une période de retournement de tendance, lorsque l’on possède simultanément des indications provenant de modèles à court, moyen et long terme.

Cependant, il est difficile de comparer les résultats de modèles efficaces sur du long terme avec ceux issus de modèles efficaces à plus court terme.

 

En rapport à ce qui a été écrit précédemment, la méthode d’Elliott semble être la méthode qui convient le mieux. Effectivement, elle peut être utilisée pour des prévisions en temps et en amplitude comprises entre quelques minutes et plusieurs années. La méthode fonctionne sur tous les marchés si ils sont efficients. Ceci est possible si on considère que l’objectif de la méthode est de modéliser le comportement psychologique des opérateurs.

 

 

La méthode d’Elliott est basée sur la reconnaissance des formes prédéterminées formées par l’évolution des cours. Pour cela, un graphique de bonne qualité est essentiel car les formes ne sont pas forcément évidentes; certains modèles décrits plus loin tel que le M.A.C.D. doivent aider à trouver les formes spécifiques. Si, à un moment donné, la configuration du marché ne correspond pas à une figure connue, mieux vaut ne pas tenter d’appliquer la méthode.

Cependant, une des propriétés majeures de cette méthode est qu’elle permet d’effectuer un analyse multi-scénarii. En effet, la pratique de la méthode consiste à se fixer une série d’objectifs en hausse ou en baisse et à considérer qu’à partir du moment ou certains seuils sont franchis, certains objectifs peuvent être éliminés, et l’évolution du marché ne peut plus être remise en cause car la configuration est parfaitement identifiée.

 

Ces configurations ( ou Patterns) sont classées en figures qui sont soumises à un certain nombre de règles. Certaines d’entre elles sont dites impératives alors que d’autres sont dites contingentes. Les règles contingentes seront exposées lors de la présentation des configurations afin de mieux coller à chaque situation. Ce mélange d’une approche objective et d’une approche intuitive est une des raisons du succès de la méthode d’Elliott sur les marchés financiers. Comme nous le verrons, le respect de ces règles permet de faire des prévisions de bonne qualité.

 

b) Terminologie

 

Avant d’aborder la théorie, nous allons donner quelques définitions des termes les plus courants dans la méthode d’Elliott.

 

· Vague :

 

A un degré donné, une vague correspond soit à la tendance principale, soit à la tendance de correction (fig. 6)

 

 

figure 6

 

 

 

·Sous-vague :   

 

Il s’agit de chacun des mouvements composant une vague.

C’est une notion relative. En effet, à un degré n, une vague est composée de sous-vagues. Mais au degré n-1, les sous-vagues précédentes deviennent des vagues. Ces vagues sont elles-mêmes composées de sous-vagues au degré n-2, etc... Ceci est valable dans tous les cas de figure, excepté le cas où l’on se trouve au plus infime degré.

 

 

· Tendance principale :

 

A un degré donné, la tendance principale sera haussière si l’amplitude mesurée pour passer de l’état survendu à suracheté est supérieure à l’amplitude mesurée pour passer de l’état suracheté à survendu suivant, c’est à dire si un mouvement de hausse et supérieur en amplitude au mouvement de baisse suivant.

Dans ce cas, la baisse s’appellera plutôt Correction.

 

La tendance principale sera baissière à un degré donné, lorsque l’amplitude de la baisse (entre l’état suracheté et survendu) sera supérieur à l’amplitude de la hausse (entre d’état survendu et suracheté) suivant.

Dans ce cas, la hausse s’appellera plutôt Reprise technique.

 

 

· Vague d’impulsion :

 

Vague allant dans le sens de la tendance principale. Un définition plus précise sera donnée plus loin.

 

 

· Vague de correction :

 

Vague allant dans le sens opposé de la tendance principale. Ce type de vague sera détaillé plus loin dans cette partie.

 

 

· Extension :

 

amplitude d’une vague ou d’une sous-vague plus importante que celle attendue (en général supérieure à 161%)

 

2.  Les règles impératives

 

Les règles impératives doivent être respectées simultanément. Si l’une d’entre elles est contredite, cela signifie qu’une erreur s’est glissée dans le raisonnement.

Nous définirons les règles impératives en cumulant le principe de la méthode d’Elliott et les règles de base.

 

a) Le principe

 

Chaque type de vague d’Elliott est composée elle-même de trois ou cinq vagues, elles-mêmes composées de sous-vagues.

 

Tout mouvement de la tendance principale se décompose en cinq vagues.

Tout mouvement de la tendance de correction peut se décomposer en trois vagues.

 

b) Les règles de base

 

Ces règles se cumulent donc au principe.

 

¨  Règle n°1

 

Pour chaque tendance principale correspond une tendance de correction. C’est à dire qu’après un mouvement dans un sens, il y a un autre mouvement en sens contraire.

 Par exemple, sur la figure 14, si l’on considère que la tendance principale est le mouvement compris entre le 13/8 et le 20/8, la correction sera enregistrée du 20/8 au 31/8. Si l’on prend pour tendance principale le mouvement compris entre le 31/8 et le 16/9, la correction se fera du 16/9 au 21/9. Enfin, pour une tendance principale entre le 13/8 et le 15/10 on constate une correction entre le 15/10 et le 4/11.

 

¨  Règle n°2

 

A un degré donné, une vague de correction doit impérativement avoir une durée comprise entre 0,38 et 1 fois celle de la vague d’impulsion précédente, sauf si la correction est un triangle en vague 4.

 Si la durée est trop courte, le décompte est faux, car il s’agit seulement de la première des trois sous-vagues qui composent la correction. En revanche, si la correction retrace totalement la vague d’impulsion, un remise en cause du décompte précédent est nécessaire (d’où l’intérêt de garder en vue l’anticipation d’un second scénario). Sur notre exemple, les ratios sont respectés.

 

¨  Règle n°3

 

La tendance principale peut avoir un cadre de durée très large comprise entre quelques minutes et plusieurs années. Afin de faciliter le repérage du type de vague dans lequel l’opérateur se situe, R.N. Elliott propose une nomenclature (fig. 7), encore respectée aujourd’hui. On distingue 9 degrés de vagues. Nous exposerons les problèmes rencontrés quant à la durée correspondant à la nomenclature.

 

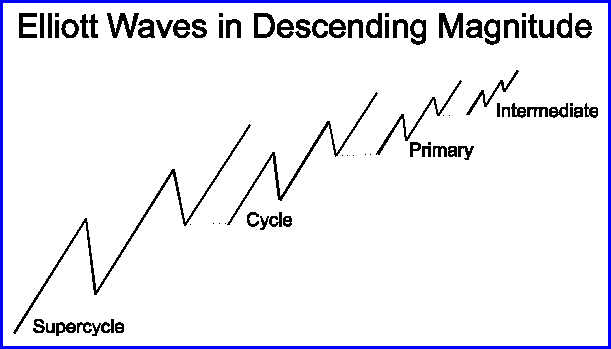
figure 7

 

 

Il est intéressant de noter que les six premier degrés, en partant de la duré la plus courte, correspondent aux niveau de saturation rencontrés dans les modèles ondulatoires, tels que le Stochastique ou le M.A.C.D. Nous verrons dans la seconde partie l’intérêt de ce rapprochement, en terme de gain d’efficacité pour la méthode d’Elliott.

 

 

 

¨  Règle n°4

 

Dans la tendance principale, les vagues sont notée de 1 à 5, alors que dans la correction les vagues sont notées de A à C (fig. 6).

 

¨  Règle n°5

 

A un degré donné, le premier mouvement est composé de cinq vagues dans la tendance principale et de trois vagues de correction. Cet ensemble représente donc la première et la seconde vague du degré supérieur (fig. 6).

 

¨  Règle n°6

 

A un degré donné dans une tendance haussière, le plancher de la vague 4 ne doit pas casser le sommet de la vague 1, sauf dans le cas d’un Triangle Diagonal (voir plus loin). De même dans une tendance principale baissière, le sommet de la vague 4 ne doit pas dépasser le plancher de la vague 1 (sauf pour un Triangle Diagonal). Cette règle est essentielle, et le non-respect de celle-ci peut entraîner des erreurs de décompte.

 

¨  Règle n°7

 

La vague 3 de la tendance principale ne peut pas être la vague de la tendance principale ayant la plus faible amplitude. Nous verrons que cette règle engendre des propriétés intéressantes dans certains cas, notamment celui de la vague d’extension.

 

¨  Règle n°8

 

Dans la tendance principale, une des trois vagues d’impulsion est en extension.

 

 

 

 

 

 

3.  La durée : une nouvelle classification.

 

a)  à propos des degrés ...

 

Nous verrons comment la méthode d’Elliott s’est adaptée aux évolutions de la sphère financière, en ce qui concerne la classification des durées et de ce qu’Elliott appelait « degré ».

 

Dans l’ouvrage d’origine, R.N. Elliott proposait des niveaux de durées échelonnés entre la journée et cinquante ans et plus. En effet, R.N. Elliott parlait de :

 

 

 

 

A titre d’exemple, nous pouvons observer la décomposition du trend du Dow Jones depuis 1920 effectuée par R. Prechter dans son ouvrage Elliott Waves Theorist (fig. 8).

 

Ceci ne correspond plus aux besoins actuels qui sont centrés sur des périodes échelonnées entre quelques minutes et quelques mois. En effet, dans la pratique, les traders n’utilisent que très rarement les grands cycles et s’arrêtent souvent au cycle primaire.

 

 figure 8

 

Ainsi de nombreux auteurs et fabricants de logiciels de trading s’accordent à penser que la grille d’origine doit être modifiée afin de la faire coïncider avec d’autres critères d’évaluation tels que l’indicateur de saturation. Dans la méthode d’Elliott, un niveau de saturation correspondra donc à un degré.

 

En dehors du problème d’exactitude des prévisions, le problème majeur des analystes est celui de la communication. Comme il n’est pas rare que sur les marchés, une personne lise un journal économique, écoute un conseil ou échange une idée avec un autre intervenant, ce point particulier est tout à fait important. Déjà, si un technicien parle de court terme, moyen terme, long terme avec un économiste ils ne parleront pas de la même chose puisque le court terme économique est en général perçu comme une durée allant de six mois à un an, alors que pour un technicien de marché trois mois représentent une période de très long terme.

 

 

 

Un des mérites de la méthode d’Elliott est de fixer un vocabulaire précis en classant le temps par des durées : ce sont les degrés.

 

 

Donc désormais, en fonction de la durée de chaque vague de la tendance principale, les traders elliottistes parleront de :

 

 

 

Dans la pratique, on part généralement du degré le plus court disponible, on applique la décomposition Elliottiste (en l’occurrence i, ii, iii, iv, v, -a-, -b-, -c-, si l’on se situe dans un degré Minute, ou bien 1, 2, 3, 4, 5, a, b, c, si l’on se situe dans un degré Mineur ), puis on remonte en suivant la formalisation jusqu’au degré le plus haut.

 

b) Application

 

Observons maintenant la figure 9.

 

figure 9

 

 

· La partie V représente les vagues (1) et (2) du degré intermédiaire. Elle forme également un degré Mineur complet : cinq vagues à la hausse (Wa) et trois vagues à la baisse (Wb).

 

· La partie Wa représente la vague (1) du degré Intermédiaire, mais aussi la tendance principale du degré Mineur. Elle est composée de cinq vagues.

 

· La partie Wb représente la vague (2) du degré intermédiaire, mais aussi la correction du degré Mineur. Elle est composée de cinq vagues.

 

· La partie Xa représente la vague 3 du degré Mineur. C’est également la tendance principale à l’intérieur de la correction, cette vague se décompose en cinq vagues et elle se note avec des chiffres (i à v).

 

· La partie Xc représente la vague B du degré Mineur. Comme il s’agit de la correction à l’intérieur d’un mouvement de correction, cette vague se décompose généralement en trois. Elle se note avec des lettres -a- à -c- .

 

· La partie Ya représente la vague iv au degré Minute. Comme il s’agit d’une vague de correction, elle est notée avec des lettres (-a-) à (-c-).

 

c)  Exemple

 

figure 10

 

Sur la figure 10, nous pouvons décomposer la tendance haussière en cinq vagues de degré Cycle :

 

Vague I ................         du 15/9/1986 à début décembre 1986

Vague II ..............          de début décembre 1986 à début janvier 1987

Vague III .............         de début janvier 1986 à début avril 1987

Vague IV .............         de début avril 1987 à fin avril 1987

Vague V ..............         de fin avril 1987 au 24 août 1987

 

 

La vague V peut se décomposer en cinq vagues intermédiaires :

 

Vague� ......................................     27/04 ð 11/05

Vague‚ ......................................     11/05 ð 21/05

Vagueƒ ......................................     21/05 ð 22/06

Vague„ ......................................     22/06 ð 21/07

Vague… ......................................     21/07 ð 24/08

 

 

figure 11

 

 

 

La vague … peut se décomposer en cinq vagues mineures (fig. 11):

 

Vague (1) .....................................    21/07 ð 03/08

Vague (2) .....................................    03/08 ð 04/08

Vague (3) .....................................    04/08 ð 17/08

Vague (4) .....................................    17/08 ð 20/08

Vague (5) .....................................    20/08 ð 24/08

 

 

III.          Les configurations

 

 

L’enchaînement des sous-vagues composant une vague, à un degré donné, forme ce que l’on nomme des figures.

 

Les figures que l’on peut rencontrer lorsque l’on utilise la méthode d’Elliott pour effectuer des prévisions sur les marchés, sont réparties en deux catégories. Les premières apparaissent lorsque l’on se trouve dans une tendance principale, qu’elle soit haussière ou bien baissière. Les autres sont celles que l’on peut observer dans une tendance de correction.

 

Chaque figure possède une dénomination précise. Dans un degré donné, le trader ne doit pouvoir déterminer qu’une et une seule figure. Ceci est un aspect très important, surtout en ce qui concerne la communication entre les différents utilisateurs. En effet, ces figures s’enchaînent selon certaines règles bien précises, et non selon une distribution aléatoire.

 

L ’objectif de tout trader est de déterminer quel type de figure le marché est-il en train de former, et d’anticiper quel va être le dénouement (en terme de temps et d’amplitude) de cette figure . Mais, la figure en question, par définition, n’arrivera pas à son terme. Par conséquent,  plus tôt le trader pourra reconnaître le type de figure, et plus il aura d’espérance de faire du profit.

 

Nous nous proposons donc de présenter ces figures, d’expliquer les règles et les directives, leur fréquence d’apparition, et d’indiquer comment elles s’enchaînent. Nous avons intégré dans les directives, tous les ratios et les règles contingentes issus d’une analyse empirique de la formation de ces configurations qui permettront de mettre en application la méthode, ainsi que les données concernant la personnalité des vagues proposées par R.N. Elliott et reprises par A.J. Frost et R. Prechter dans Elliott Waves Principle.

 

 Cette partie sera aussi réalisée grâce aux sources les plus récentes possibles, à savoir les publications de « La Synthèse Financière » du Service d’Etudes en Finance Internationale (S.E.F.I), ainsi que des rapports directs avec The Center for Elliott Waves Analysis.

 

Par souci de clarté, nous présenterons dans une première partie les figures de correction, et dans une seconde les figures d’impulsion.

 

1.  Les figures de correction

 

Ces figures se forment lorsque les cours évoluent dans le sens inverse de la tendance principale.

L’étude de ces configurations ne nécessitant pas de connaissance des figures d’impulsion, c’est la raison pour laquelle il est opportun de les présenter en premier.

Les vagues correctives sont moins faciles à identifier et à décomposer que les vagues d’impulsion. Pour cette raison, il est parfois difficile d’identifier le schéma de la vague de correction avant son achèvement. Comme il est aussi plus difficile de cerner la fin des vagues correctives que celle des vagues d’impulsion, l’analyste doit être plus attentif quand le marché est « dans les eaux troubles ».

 

Cette complexité est due au plus grand nombre de cas d’espèces pour les vagues correctives que pour les vagues de hausse. En effet, une correction peut se limiter à une simple consolidation ou au contraire épouser des allures beaucoup plus dévastatrices et incertaines.

 

Comme nous le verrons, l’étude des différentes configurations ne permet de tirer qu’une seule règle vraiment importante : une correction ne peut jamais être en cinq. En d’autres termes, un mouvement initial en cinq contre la tendance générale n’est jamais la fin d’une correction, mais seulement partie de celle-ci.

 

On distingue généralement quatre groupes de schémas de corrections.

 

ÄLes Zig-Zags (5-3-5);

ÄLes corrections à plat ou Flats (3-3-5); ce groupe inclut entre autres les Flats « courants » et les Poussées

ÄLes Triangles (3-3-3-3-3); ce groupe inclut quatre variétés: « ascendant », « descendant », « fermé » et « ouvert »;

 

 

 

 

Caractéristiques générales et objectifs de correction :

 

 

· Les sous-vagues de ces figures sont notées A, B et C.

 

· L’amplitude de ces corrections dépend des ratios de Fibonacci, décrits plus haut : 38%, 50%, 62%, 100%, mais il est également possible de rencontrer 23% et 76%.

Ainsi, quand on sait qu’une vague d’impulsion a pris fin, il est possible de déterminer des objectifs de correction.

 

 

Prenons un exemple. Supposons que la vague 1 a été caractérisée par une hausse des cours d’une valeur de 100 à une valeur de 140. Dans ce cas , si on considère que la vague 2 est généralement lus dévastatrice sur les marchés, et donc qu’une correction supérieure à 50% est la plus souvent observée, les objectifs possibles pour la vague 2 sont les suivants :

 

 

 

% de Correction	Taille de la vague 2	Objectif
50%	20	120
62%	24.8	115.20
76%	30.8	109.20
100%	40	100

 

 

Remarque:

 

Elliott fournit une étude détaillée de la personnalité des vagues dont nous n’exposerons pas les détails. Cette étude permet d’appréhender de manière relativement exacte l’état du marché suivant la vague sur laquelle on se situe. De plus, elle caractérise de manière précise chaque vague et permet d’éliminer systématiquement des anticipations d’objectifs, tout simplement parce elles ont probabilité infime de se réaliser au regard des évolutions passées.

 

 

 

Illustration :

 

 

 

Nous allons maintenant présenter les différents types de configurations que l’on peut trouver dans une correction.

 

a) Le Zig-Zag (5-4-5)

 

 

 

 

Représentation :

 

 

figure 12

 

 

Règles :

 

· Un Zig-Zag dans un marché haussier est toute figure simple en trois vagues se subdivisant en 5-3-5 avec un sommet de la sous-vague B nettement plus bas que le début de la sous-vague A.

 

· Dans un tendance principale qui évolue dans une direction, une correction en Zig-Zag sera dans la direction opposée.

 

· La vague A est une Impulsion standard.

 

·La vague C est une Impulsion standard ou bien un Triangle Diagonal.

 

· La vague B corrige faiblement la vague A (d’une amplitude a peu près égale à 50 ±12% de la vague A).

 

· La vague C enfonce largement le bottom de la vague A

 

 

Directives :

 

· La vague C a de fortes chances d’être égale à la vague A en amplitude.

 

· En règle générale l’amplitude des vagues A et C est généralement reliée par un ratio de Fibonacci (la plupart du temps 0,618; 1 ou 1,618). Il est donc possible, grâce à cette règle ajoutée à celle concernant toutes les corrections (voir plus haut), de déterminer des objectifs pour la fin de la vague C (voir les spécificités).

 

· Si l’on observe une vague C beaucoup plus longue que 161,8% de la vague A, on a une grande probabilité qu’il s’agisse des vagues 1, 2 et 3 d’une impulsion plutôt que les vagues A, B et C d’un Zig-Zag.

 

· Si la vague C est plus abrupte que la vague A, alors la configuration a de fortes chances d’être en réalité un Double ou Triple Zig-Zag.

 

 

Cas particulier :

 

On rencontre parfois une catégorie particulière de Zig-Zags : les Double Zig-Zags. Il s’agit de deux Zig-Zags successifs interrompus par une petite correction en trois vagues a, b, c. Deux formalisations sont alors possibles pour caractériser la séquence : la première est de considérer l’ensemble comme une vaste correction en A, B, C dont chaque vague est formée de trois vagues mais dont les vagues A et C sont des Zig-Zags. La seconde formalisation considère qu’il s’agit d’une double correction en Zig-Zag interrompue par une petite reprise.

 Mais ces cas de figure sont rares, il est donc inutile de s’attarder sur ce point précis.

 

spécificité :

 

Si le Zig-Zag est une vague 2, en général il corrigera 61,8% de l’amplitude de la vague 1

Si le Zig-Zag est une vague 4, il peut se terminer au niveau du sommet de la vague 1 de même degré. De plus on observe que dans 80% des cas, si la vague 2 était un Flat, alors le Zig-Zag aura une amplitude de 200% du Flat et une durée de 50% de la durée du Flat (fig. 14).

 

 

Localisation :

 

La Zig-Zag se place en vague 2 ou 4. Le mouvement d’impulsion qui le suit n’est, dans la plupart des cas, pas en extension. Si, en vague 2, on a eu un flat, on a 80% de chances d’avoir un Zig-Zag en vague 4. Ce qui est le cas de la figure 14.

 

b) Le Flat

 

 

 

C’est la figure la plus facile à repérer. Elle se décompose en 3 vagues A, B et C, d’amplitudes équivalentes.

 

Représentation :

 

 

 

 

Règles :

 

· La première vague est formée de 3 sous-vagues comprises entre 0 et A. Le plus souvent, il s’agit d’un Zig-Zag.

 

· La seconde est également composée de 3 sous-vagues. Là aussi, il s’agit le plus souvent d’un Zig-Zag. Cette seconde vague se caractérise par le fait qu’elle se termine au niveau du début de la première vague de correction, c’est à dire au début de la correction. On fixe comme limite que la vague B retrace la vague A d’au moins 61,8%.

 

· La troisième vague se décompose en 5 vagues et se termine au niveau de  A, ou retrace au moins 61,8% de la vague B. La plupart du temps, il s’agit d’un Impulsion standard.

 

Dans la mesure ou cette configuration est la plus facile a identifier et la plus simple du point de vue de la construction, il est inutile de présenter des directives utiles pour prévoir et contrôler l’évolution de la figure en cours d’identification. En particulier, l’objectif pour la vague C sera le niveau de la vague A  ±38,2%.

 

 

Spécificité :

 

Si au point B, le sens du marché s’inverse, une position peut être prise avec pour objectif le bottom de la vague A. Si à ce niveau, un décompte de 5 est effectué et que la marché se retourne, une position dans le sens de la tendance principale pour une amplitude comprise entre 100% à 161,8% de la vague d’impulsion précédente doit être prise.

En effet, le Flat précède ne général une vague en extension, c’est à dire d’amplitude supérieure (161% environ) aux autres vagues d’impulsion.

 

 

Localisation :

 

Si un flat a lieu en vague 2, un Zig-Zag est attendu en vague 4, dans 80% des cas (fig. 14). L’inverse se produit également : si un Zig-Zag a été observé en vague 2, alors on aura de fortes chances d’avoir un flat en vague 4, surtout si la vague 3 n’a pas connu d’extension.

 

c)  La Poussée

 

 

Représentation :

 

 

 

· La première sous-vague est composée de trois sous-vagues entre les sommets de la vague 1 et de la sous-vague A. Elle peut former un Zig-Zag, mais la durée sera trop faible par rapport à la vague précédente pour faire partie du même degré.

 

·La seconde sous-vague est également composée de trois sous vagues ; mais, à la différence du Flat, le point B se situe au-dessus du sommet de la vague 1, départ de la vague de correction.

 

·La troisième sous-vague est une Impulsion standard composée de cinq sous-vagues comprises entre les points B et C=2.

 

Spécificité :

 

La spécificité de cette figure vient du fait que la point B, qui marque la fin de la seconde sous-vague, se situe bien au-dessus du sommet 1. De même, dans la plupart des cas, le point C=2 se situe au-dessus du sommet 1, c’est à dire que la fin du mouvement de correction se situe au-dessus du sommet de la vague 1, lorsque la tendance est à le hausse. Cette notion peu orthodoxe déroute souvent les non-initiés.

Le mouvement d’impulsion qui suit cette vague est en général sans précédent pour sa violence de réaction.

Sa structure est donc très caractéristique.

 

Localisation :

 

Bien qu’elle puisse se situer en vague 2, sa place habituelle est en vague 4. En outre, on ne note sa présence que très rarement lorsque la tendance est à la baisse.

 

d) Les Triangles

 

 

Représentation :

 

 

 

 

 

 

 

 

Règles :

 

· Les Triangles sont formés de cinq sous-vagues de trois dont l’amplitude devient de plus en plus réduite, sauf dans le cas des Triangles en formation élargie.

 

· On distingue 4 types de Triangle: Les Triangles descendants, ascendants , symétriques et inversés. ces figures sont issues des la théorie de Charles Dow.

 

· Les mouvement en Triangle correspondent généralement à des consolidations limitées (corrections inférieures à 50% et souvent proches de 38%). Elles indiquent qu’il existe une certaine indécision du marché et qu’il a besoin de se reposer légèrement avant de poursuivre sa tendance.

 

 

Directives :

 

· Les vagues sont en général liées entre elles par le Nombre d’Or

 

· La rupture de la droite de résistance du Triangle entraîne souvent un mouvement brutal. L’objectif se calcule comme dans tous les triangles chartistes, en reportant la base du triangle au point de franchissement de la résistance.

 

 

Spécificité :

 

· On reconnaît souvent les formation en Triangle grâce à l ’existence de nombreux gaps non significatifs produits sans volume.

 

· Il s’agit d’une figure assez rare. Avant de confirmer que l’on a un triangle, il est recommandé de remettre en question le décompte.

 

 

Localisation :

 

· Les Corrections en Triangle arrivent souvent avant le dernier mouvement terminal. On les retrouve donc pratiquement toujours en vague 4 et quelquefois en vague B.

2.  Les figures d’impulsion

 

 

Les vagues d’impulsion ne peuvent être qu’en cinq. Les sous-vagues de ces figures seront notées 1, 2, 3, 4, 5…

 

En règle générale, on peut dire que parmi les trois vagues d’impulsion 1, 3 et 5, deux vagues ont des amplitudes équivalentes et une vague est en extension. Si la vague trois est en extension et qu’elle est suivie par une figure de type « Poussée », la vague 5 peut être en extension par rapport à la vague trois. Ce cas reste tout de même l’exception.

 

a) L’Impulsion Standard

 

 

Représentation :

 

figure 13

 

Règles :

 

· La vague 1 est une vague d’impulsion de type Impulsion standard ou bien Triangle Diagonal ;

 

· La vague 2 est une vague de correction de tout type, qui ne doit pas retracer totalement la vague 1, en amplitude ;

 

·  La vague 3 doit être une Impulsion standard, qui doit être plus longue, en amplitude, que la vague 2. La vague 3 ne doit pas être la vague d’impulsion la plus courte en amplitude (par rapport aux vague 1 et 5) ;

 

· La vague 4 est une vague de correction de tout type, dont le niveau final ne doit pas être inférieur au niveau du sommet de la vague 1 ;

 

· La vague 5 doit être une vague d’impulsion de type Impulsion standard ou bien Triangle Diagonal, qui doit représenter en amplitude au moins 38,2% de la vague 4 .

 

Directives :

 

· La vague 1 est la plus souvent une Impulsion standard, mais ce n’est que très rarement un Triangle Diagonal (voir plus loin) ;

 

· La vague 2 est une vague de correction de la précédente. Elle se décompose en trois sous-vagues. Il peut s’agir, soit d’un Flat, soit d’un Zig-Zag, soit d’un Double Zig-Zag, soit d’un Triple Zig-Zag, mais ce n’est que très rarement un Triangle ;

 

Ü Il a été observé qu’en règle générale, mais ce n’est pas systématiquement le cas,

 

Ä si la vague 2 est un Zig-Zag, la vague 3 sera de longueur équivalente à la vague 1 ;

Ä si la vague 2 est un Flat, la vague 3 a une forte probabilité d’être en extension.

 

· Généralement, la vague 2 retrace la vague 1 d’au moins 23,6%. Mais, le plus souvent, la vague 2 retracera 38,2%, 50% ou 61,8% de l’amplitude gagnée par la vague 1, et elle ne doit en aucun cas retracer la totalité de la vague 1 ;

 

· La durée de la vague 2 correspond environ à 50% du temps pris par le marché pour réaliser la vague 1. Mais, dans tous les cas, la durée de la vague 2 ne peut pas excéder celle de la vague 1 ;

 

 

 La vague 3 est au moins égale à la vague 1 et elle est très souvent en extension, surtout lorsque la vague 2 est un flat (sauf dans le cas de marchés de « commodities » et de Futures, ou la vague qui est le plus souvent en extension est la vague 5); Dans ce cas, l’amplitude attendue pour cette vague pourra être 161,8% ou 262,8% de l’amplitude de la première vague ;

 

 

· La vague 4 est à mettre en relation avec la vague 2 :

 

                   Ä Dans 80% des cas,

               

si la vague 2 est un Zig-Zag, la vague 4 sera un Flat ;

si la vague 2 est un Flat, la vague 4 sera un Zig-Zag.

 

       Ä Les rapports d’amplitude et de durée des vagues 2 et 4 sont de 50%, 100% et 200%. Généralement, les ratios d’amplitude et de durée sont inversés ;

 

Sur l’exemple fig. 14,

 

en amplitude, la vague 4 représente 200% de la vague 2 :

en durée,        la vague 4 représente 50% de la vague 2.

 

 

·      La vague 5 est en principe équivalente à la vague 1. Cependant, si la première et la troisième vague d’impulsion ont des amplitudes comparables et si la quatrième vague est un flat, alors la probabilité augmente pour que la cinquième vague soit en extension. Dans ce cas, le niveau attendu à la fin de la vague 5 pourra être 161,8% de l’amplitude mesurée entre le début de la vague 1 et la fin de la vague 3 ;

 

· Il faut noter que dans une Impulsion standard, on rencontre très généralement le couple Flat / Zig-Zag accompagné d’une vague 1 et 5 de même amplitude et d’une troisième  vague d’amplitude supérieure.

 

figure 14

 

 

 

Spécificité :

 

Cette vague Impulsion standard est typique des débuts de mouvement.

 

 

Localisation :

 

Cette vague standard se rencontre surtout en vague (1), mais peut également se rencontrer en vague (3), si la vague (2) était un Zig-Zag, ou bien en vague (5), si la vague (4) était un Zig-Zag et s’il s’agit de la vague 1.

b) L’extension

 

 

Cette vague est le deuxième type de vagues d’impulsion.

 

Le plus souvent, les formations en cinq vagues sont faciles à repérer, mais il y a quelque fois des irrégularités appelées Extensions. Les Extensions sont assez fréquentes. Il s’agît d’exagérations ou d’élongations, généralement dans l’une des trois vagues d’impulsion (1, 3 ou 5).

 

Nous verrons que l’existence d’extension peut s’avérer utile dans la détermination de la longueur probable des vagues futures.

 

 

 

Règles :

 

 

· Ce type de vague se différencie de l’Impulsion standard par le fait que la vague d’impulsion la plus importante est beaucoup plus grande que 161,8% de la vague en extension de base. Parfois, les subdivisions d’une extension ont presque les mêmes amplitudes et durées que les quatre vagues principales, ce qui donne un total de neuf vagues de taille équivalente au lieu du décompte normal en cinq de la séquence. Il est alors parfois difficile de savoir laquelle des neuf vagues est une Extension. Mais ceci est toutefois sans importance, car les décomptes en cinq ou en neuf ont les mêmes implications techniques dans le système d’Elliott. Les diagrammes de la figure ? illustrent des extensions et devraient clarifier ce point.

 

· Bien qu’en théorie, elle puisse se situer indifféremment dans n’importe laquelle des trois vagues d’impulsion, les extensions les plus fréquentes se situent en vague 3 ou 5. En effet, une extension sur la vague 3 est très fréquente dans l’analyse des marchés des actions, et une extension  sur la vague 5 est très fréquente dans le cas de marchés des « biens ».

 

 

Représentation :

 

 

figure 15

 

 

Directives :

 

 

· Taille des vagues en Extension :

 

Nous avons vu que R.N. Elliott considérait que Fibonacci avait fortement influencé sa théorie. En fait, dans la méthode des vagues d’Elliott, la taille relative des extensions se calcule grâce au « Nombre d’Or de Fibonacci ».

 

 

Ce ratio va permettre de calculer des objectifs de prix dans le cas de figures d’extension. En effet, dans la majorité des cas, une vague en Extension aura une taille qui sera proche de 161,8% ou 200% de la taille des deux autres vagues. Par conséquent, les ratios correspondant à la taille relative des vagues tendront vers :

 

Vague 1	Vague 3	Vague 5
A > 161,8%	100%	100%
100%	A’ > 161,8%	100%
100%	100%	A’’ > 161,8%

 

John J. Murphy, dans son ouvrage Technical Analysis of the Futures Markets, décrit la manière dont il fait usage du Nombre d’Or pour calculer des objectifs, ou plutôt des intervalles d’objectifs. Pour cela, l’auteur présente une série de quatre règles, desquelles nous allons donner une description détaillée.

 

 

Œ Nous avons déjà vu que dans la méthode d’Elliott, une extension ne se produit généralement que sur une des trois vagues d’impulsion et que la vague 1 est très rarement en extension. Donc, si une de ces vagues connaît une extension les deux autres doivent avoir la même taille, tout spécialement si les volumes sont plus importants en vague 5 qu’en vague 3. Ceci implique des conséquences intéressantes en ce qui concerne la prévision (fig. 16):

 

Ä si la vague 3 est en extension, la vague 5 aura tendance à ressembler à la vague 1 ;

Ä si les vagues 1 et 3 sont des Impulsions standards, la vague 5 aura de fortes chances d’être en extension.

 

 

� Une cible minimale pour le sommet de la vague 3 peut  être calculée en multipliant la longueur de la vague 1 par 1,618 et en additionnant le tout au niveau de la fin de la vague 2.

 

figure 16

 

 

Ž Le niveau du sommet de la vague 5 peut aussi être prévu ou du moins approché (fig. 17). En effet, J.J. Murphy calcule des cibles maximales et minimales pour ce point.

La cible maximale est calculée en ajoutant au sommet de la vague 1, 3,236 (qui correspond au double du Nombre d’Or) fois l’amplitude mesurée de cette même vague 1.

La cible minimale est calculée en ajoutant 3,236 fois l’amplitude de la vague 1, cette fois à la base de la vague 1.

 

figure 17

 

 

� Lorsque l’on a observé des vagues 1 et 3 d’une amplitude plus ou moins égale et, par conséquent, que l’on s’attend à ce que la vague 5 soit en extension, il est aussi possible de calculer un objectif de prix (fig. 18).

Il faut mesurer l’amplitude observée entre le bas de la vague 1 et le sommet de la vague 3, puis ajouter 1,618 fois cette amplitude au bout de la vague 4.

 

 

figure 18

 

 

Spécificité :

 

Les information qui permettent de reconnaître cette figure avant qu’elle ne soit terminée - puisque tel est l’objectif - sont :

 

· augmentation des volumes de transactions ;

· formation de gaps ;

· hausse des positions ouvertes (dans le cas de contrats Futures).

 

Si l’extension se situe en vague 3, elle est en général suivie d’un Zig-Zag en vague 4.

 

 

 

Localisation :

 

Dans la tendance principale, une des trois vagues d’impulsion est toujours en extension. Elle succède systématiquement à une poussée (voir plus loin), sinon elle peut se produire après un flat, mais très rarement après un Zig-Zag.

Elle se situe en vague 5, s’il n’y en a pas eu en vague 1, ou en vague 3 de la tendance principale.

 

 

 

figure 19

 

c)  La Cassure

 

 

Elliott a utilisé le mot « Failure » (qui signifie littéralement « invalidation ») pour décrire un schéma en cinq vagues dont la vague 5 n’arrive pas à dépasser le plus haut (resp. bas) de la vague 3 dans un marché haussier (resp. baissier).

 

 

Représentation :

 

 

 

 

Règles :

 

Comme les autres vagues d’impulsion, elle se découpe en 5 vagues.

 

 

 

 

· La première vague est du type Impulsion Standard.

 

· La deuxième vague est une vague de correction sans spécificité.

 

· La troisième vague peut, dans certains cas être d’amplitude inférieure à le première. Par conséquent, comme nous avons vu que la troisième vague ne peut pas être la plus courte des trois vagues d’impulsion, cela renforce la probabilité que l’on soit en présence d’une Cassure.

 

· La quatrième vague ne présente pas de particularité.

 

· En revanche, la cinquième vague se singularise par la faiblesse de son amplitude. Celle-ci est telle qu’en général le sommet de la vague 5 se situe en dessous  ou au niveau du sommet de la vague 3 dans une tendance haussière et au dessous du sommet de la vague 3 dans une tendance principale baissière.

 

figure 20

 

 

 

Spécificité :

 

Les Cassures sont les signes avant-coureurs de la force ou de la faiblesse sous-jacente du marché; elles donnent alors bien plus d’informations que la majorité des traders veut bien entendre. En effet, juste au moment où ceux-ci pensent que « tout est bien emballé » sous l’étiquette Elliott, arrive une Cassure qui « coupe l’herbe sous le pied à l’objectif escompté », selon les termes de A.J. Frost.

En réalité, une cassure annonce un retournement de tendance important. L’analyse des volumes de transactions et des indicateurs (par exemple, le Momentum ou bien  le M.A.C.D.) sont d’une aide précieuse pour la détecter.

 

 

Localisation :

 

Les Cassures sont fréquentes, spécialement dans les vagues de degré Cycle ou bien Primaire. Elle se situe en fin de vague 5 lorsqu’elle est dans une tendance principale ou en fin de vague C lorsqu’elle est dans une tendance de correction.

 

 

d) Le Triangle Diagonal

 

 

 

 

Les Triangles Diagonaux (ou Biseaux† ) apparaissent en vague 5 après que la mouvement initial soit allé « trop vite trop loin » ainsi qu’Elliott l’indiquait, c’est à dire après avoir connu un vague 3 particulièrement efficace.

 

Ils constituent un type spécial de vague 5 qui indique l’épuisement du mouvement de fond. Arrivé en fin de mouvement, le marché a alors du mal à atteindre un nouveau sommet significatif.

 

 Les Triangles Diagonaux sont des biseaux formés par deux lignes (ou « Channel Lines ») convergentes, chaque sous-vague, y compris les vagues d’impulsion, se subdivisant en trois‡ , comme illustré figure 21.

 

 

figure 21

 

 

Règles :

 

 

· Un Triangle Diagonal évolue entre deux « Channel Lines ». La première, la ligne de résistance , relie les sommets des vagues 1 et 3. La seconde , la ligne de support, relie les sommets des vagues 2 et 4. Dans de rares cas, les traders acceptent un dépassement de 15% de l’amplitude.

 

· Ce type de figure n’est pas commun, mais dans presque tous des cas, on a affaire à une configuration 3-3-3-3-3 (voir fig. 22)

 

· L’intersection des deux « Channel Lines » doit s ’effectuer après la fin de la figure.

 

· Les vagues 2 et 4 doivent se superposer d’au moins 10%, en amplitude.

 

 

Directives :

 

· Un Triangle Diagonal ascendant est baissier. Généralement, une forte baisse suit, au moins jusqu’au niveau du début du Triangle Diagonal.

 

· Un Triangle Diagonal descendant est donc par conséquent haussier.

 

· La rupture de la droite de support (ou de résistance) confirmera ensuite la fin de la tendance et l’amorce du retournement.

 

· Dans la plupart des cas, la vague 4 enfonce le top (ou le bottom) de la vague 1. C’est une des seules figures ou ce cas eut se produire.

 

· Comme dans le cas d’une Impulse, la vague 4 est à mettre en relation avec la vague 2 :

 

                   Ä Dans 80% des cas,

               

si la vague 2 est un Zig-Zag, la vague 4 sera un Flat ;

si la vague 2 est un Flat, la vague 4 sera un Zig-Zag.

 

       Ä Les rapports d’amplitude et de durée des vagues 2 et 4 sont de 50%, 100% et 200%. Généralement, les ratios d’amplitude et de durée sont inversés ;

 

· La vague 5 pourra avoir une amplitude d’au moins 61,8% de celle de la vague 4.

 

 

 

 

exemple :

 

voir figure 22

 

 

Calcul d’objectif :

 

· Les indication en ce qui concerne les objectifs de cours de la sortie du Triangle Diagonal ne sont valables que si la sortie s’effectue dans les trois premiers quarts du Triangle.

 

· De même, les volumes doivent suivre une certaine évolution. Tout au long de la figure en Triangle Diagonal, les volumes sont peu élevés, ce qui correspond à une phase de consolidation où le marché se cherche.

La sortie du Triangle Diagonal doit s’accompagner d’une nette reprise des volumes, signe d’un regain d’intérêt pour le marché de la plupart des opérateurs.

 

Le calcul d’objectif, en analyse chartiste, est très proche d’une figure à l’autre, car reposant sur la même logique : Ici, il faudra reporter la hauteur du Triangle Diagonal à sa base, à partir du point de rupture (fig. 23).

 

 

 

figure 22

 

 

figure 23

 

 

Dans la méthode d’Elliott, pour chaque action, il y a une réaction. Une vague d’impulsion est par conséquent immédiatement suivie d’un mouvement en sens contraire, i.e. d’une vague de correction. Par conséquent, lors d’un retournement de tendance, il est important de connaître les différents types de vague de correction afin de construire plusieurs scénarii.

 

 

IV.          Une Nouvelle Approche De La Méthode D’Elliott : L’Utilisation De L’Indicateur De Saturation

 

A.          Introduction

 

L’utilisation des indicateurs de puissance fournit un apport considérable aux utilisateurs de la méthode d’Elliott. Mais, les oscillateurs (ou indicateurs de puissance) sont nombreux et divers et ne possèdent pas les mêmes capacités et la même souplesse d’utilisation.

 

S’il est utile de focaliser sur le ou les modèles ondulatoires les plus efficients, il est aussi nécessaire de présenter la philosophie générale commune à l’ensemble de ces outils.

 

Pour cette raison, nous traiterons dans un premier temps de la philosophie générale qui anime la plupart des oscillateurs (principes de base, signaux communs). Ensuite, nous présenterons deux modèles: le Stochastique et le M.A.C.D ainsi que la notion d’indicateur de saturation qui en découle. Enfin, nous verrons comment l’utilisation de l’indicateur de saturation peut réduire les risques d’erreur dans la méthode d’Elliott.

 

1.  Principes de base des oscillateurs

 

Un oscillateur peut être défini comme la dérivée d’un cours. En effet, les données de cours sont transformées par la fonction spécifique au modèle en une nouvelle série de données oscillant autour d’un niveau précis.

Les oscillateurs sont représentés en dessous des cours et peuvent être analysés techniquement

 

Un oscillateur permet de déterminer les tensions du marché.

Si l’on comparaît à la physique, la vitesse (dérivée première de l’évolution d’un mobile) permet à elle seule de comprendre le déplacement du mobile dans l’espace. Les indicateurs techniques vont permettre de repérer la puissance du mouvement comme le fait la vitesse. Leur montée indiquera le début du mouvement, leur baisse signifiera l’essoufflement du mouvement, enfin le passage du 0 (ou d’un autre niveau de référence) marquera le retournement du marché.

Mais les mouvements des marchés étant plus chaotiques que ceux des mobiles, il sera nécessaire d’effectuer des filtrages (notamment grâce à des moyennes mobiles des oscillateurs).

 

2.  Les principaux signaux fournis par les oscillateurs

 

On distingue trois grandes classes de signaux :

 

Ü le degré de surachat et de survente, représentant la tension du

    marché.

Ü les divergences avec les cours, représentant l’essoufflement du

    marché.

Ü les tendances et les figures chartistes directement appliquées au

    courbes des oscillateurs.

 

· Lorsque le marché est suracheté (resp. survendu), l’oscillateur se situe sur sa borne supérieure (resp. inférieure). Lorsque l’on utilise la moyenne mobile de l’oscillateur, on dira que le marché est suracheté (resp. survendu) lorsque la moyenne mobile passe au-dessus (resp. en-dessous) de l’oscillateur (fig. 24).

Mais, constater qu’un marché est suracheté  (resp. survendu) ne constitue pas un signal de vente (resp. achat). Cela doit au contraire servir à éviter les erreurs : il est généralement déconseillé d’acheter (resp. vendre) sur un marché suracheté (resp. survendu).

 

 

figure 24

 

· Il s’agit du point le plus intéressant des oscillateurs, les divergences constatant un situation qui n’est pas toujours directement visible sur la courbe des cours.

Une divergence représente une déconnexion entre l’évolution des cours et de l’oscillateur. On parlera de divergence baissière dans un marché suracheté si le niveau de surachat est moins élevé que le niveau de surachat précédent, et si les cours se situent à un niveau supérieur à ceux constatés lors du surachat précédent (fig. 25).On raisonne à l’inverse pour une divergence haussière dans un marché survendu.

 

 

figure 25

 

Une divergence traduit un essoufflement du marché : la vitesse du marché ralentit, ce qui permet l’apparition d’un trend baissier sur l’oscillateur, avant même que les cours n’en aient donné l’impression.

De même que précédemment, constater une divergence baissière (resp. haussière) ne constitue pas un signal de vente (resp. achat), mais doit seulement inciter à la prudence et à la prise de bénéfice.

 

· Il est aussi possible d’appliquer tous les élément de l’analyse technique au courbes même des oscillateurs.

Par exemple, grâce aux tracés de droites de support et de résistance, il sera intéressant de déterminer des tendances (trends). Ce point permettra d’affiner l’appréciation du degré haussier d’un trend et de son ralentissement (mais pas forcément de son retournement).

Aussi, il est possible d’appliquer tout la panoplie des configurations disponibles dans l’analyse chartisteˆ . Ainsi, un Head&Shoulders peut être observé sur les oscillateurs et marquer ainsi un éventuel retournement du marché.

 

 

Il est enfin possible de filtrer les oscillateurs, comme on le fait sur les cours, par le calcul de moyennes mobiles. Ce filtrage a pour principal intérêt de permettre de déceler des changements dans l’évolution de la vitesse du cours de façon assez rapide et avant même que des tendances ou des figures puissent se dessiner. Cependant, comme les moyennes mobiles utilisées sur les cours, le plus dur est trouver la « bonne moyenne » mobile, c’est à dire avec le retard opportun.

 

 

Cette présentation générale des oscillateurs ne permet pas de trancher entre plusieurs d’entre eux.

 Cependant, pour un utilisateur de la méthode d’Elliott, l’intérêt peut être porté sur deux d’entre eux, le Stochastique et le M.A.C.D. car ce sont tous deux des indicateurs objectifs car les signaux d’achat et de vente sont générés lorsqu’il y a croisement de l’indicateur et de leur moyenne mobile. De plus, ce sont des modèles qui fonctionnent parfaitement sur toute la gamme de périodes comprises entre le tic et la base mensuelle.

Nous verrons que l’utilisation simultanée de ces deux oscillateurs réduit les erreurs dans le sens où le second a un décalage par rapport au premier, et par conséquent confirme ou infirme les signaux de celui-ci.

 

 

B.          Présentation du modèle M.A.C.D. (Moving Average Convergence Divergence)

 

1.  Définition

 

L’indicateur M.A.C.D. est un indicateur obtenu à partir de la différence de deux moyennes mobiles. Il se situe sur les écrans de trading en-dessous ou au-dessus de l’indicateur stochastique.

Cet indicateur permet de profiter de la quasi totalité d’un mouvement lorsqu’il y a une forte volatilité sur les cours (décalages importants).

 

2.  Construction

 

Sa construction s’effectue en suivant trois étapes :

 

Ü Calcul de deux moyennes exponentielles MEC_t et MEL_t, à l’aide de deux facteurs de pondération. On choisira par exemple respectivement pour MEC_t et MEL_t les coefficients FP₁=0,182 et  FP₂=0,0952 correspondant respectivement à 12 et 20 périodes.

 

 

Soit C_t le cours de clôture au temps t ;

Soit MEC_t la moyenne exponentielle courte (à 10 périodes au temps t) ;

 

avec Facteur de Pondération

 

Soit MEL_t la moyenne exponentielle longue (à 20 périodes au temps t) ;

 

avec Facteur de Pondération

 

 

Ü On définit ensuite MACD_t , la différence entre les deux moyennes mobiles au temps t ; la courbe MACD_t peut être tracée sur un graphique et s’interprète comme un oscillateur de moyenne mobiles exponentielles. En comparaison de l’indicateur stochastique, le MACD_t est équivalent à %K.

 

Soit MACD_t l’indicateur MACD au temps t ;

 

 

 

Ü Puis, on calcule MACD^*_t , la moyenne mobile exponentielle de MACD (avec le coefficient FP₃= 0,0645 correspondant à une durée de 30 périodes). En comparaison de l’indicateur stochastique, le MACD^*_t est équivalent  %K.

On trace alors sur le système graphique les courbes MACD_t et MACD^*_t.

L’objet de cette dernière moyenne mobile est d’accélérer le signal donné par l’oscillateur de moyennes mobiles : La courbe MACD^*_t croisera la courbe MACD_t avant qu’elle ne passe la ligne du 0.

 

Soit MACD^*_t la moyenne mobile du MACD_t ;

 

 

 

avec Facteur de Pondération

 

 

figure 26

 

La présentation initiale de cet oscillateur montrait les deux moyennes mobiles se croisant mutuellement (cf. fig. 26). Avant chaque signal (croisement des moyennes mobiles entre elles), les moyennes mobiles avaient tendance à converger pour ensuite (après le croisement) diverger de nouveau.

 

Cette succession de croisement et donc de convergences-divergences des moyennes mobiles entre elles explique ainsi le nom de cet oscillateur : Moving Average Convergence Divergence.

 

Cette présentation a été ensuite remplacée par un histogramme montrant la différence des deux moyennes mobiles (cf. fig. 27).

 

 

Les signaux d’achat (resp. vente) sont ainsi donnés quand le SIGNAL_t devient négatif (resp. négatif).

 

figure 27

 

Cette présentation possède de nombreux mérites :

 

· les signaux d’achat et de vente générés par l’oscillateur sont particulièrement lisibles ;

· les divergences avec les cours peuvent être facilement repérées ;

· les situations éventuelles de surachat-survente sont directement visibles.

 

 

3.  Avantages du modèle M.A.C.D.

 

· Ce modèle fonctionne parfaitement à tous les niveaux de l’indicateur de saturation.

· S’il est utilisé avec le stochastique, le taux d’erreur est très faible.

· Il est plus facile à utiliser que les stochastiques entre les états surachetés et survendus.

 

4.  Inconvénient du modèle M.A.C.D.

 

· Les signaux de surachat et de survente à un niveau donné sont généralement un peu en retard par rapport à ceux du stochastique‰ .

 

5.  Application du modèle M.A.C.D.

 

 

 

6.  Conclusion

 

 

L’utilisation temporelle du M.A.C.D apporte à des moments stratégiques, période de retournement de tendance, une indication claire. Cependant, le rôle de ces modèles ne s’arrête pas là. Il sont aussi d’une grande utilité dans la méthode d’Elliott car ils permettent de délimiter les vagues. Le rôle de l’indicateur de saturation est donc très important lors de l’élaboration de stratégies et des phases de contrôle.

 

C.          Présentation du Stochastique

 

1.  Définition

 

Les oscillateurs stochastiques inventés par Georges Lane sont constitués d’un premier oscillateur, le %K, qui est ensuite filtré par un deuxième oscillateur, le %D.

2.  Construction

 

L’oscillateur %K se définit ainsi :

 

 

avec C ; dernier cours de clôture

       L_x ; cours le plus bas des x dernières périodes.

       H_x ; cours le plus haut des x dernières périodes.

 

 

 La formule permet ainsi à l’oscillateur d’évoluer entre 0 et 100. Quand le marché est au plus bas : (C - L_x) tend vers 0 et l’expression également. Inversement, quand le marché est au plus haut, le cours de clôture tend vers le niveau le plus haut des x dernières périodes, alors

 

  et l’oscillateur %K tend donc vers 100

 

 

 

Le second oscillateur %D lisse le %K par la formule suivante :

 

 

où    H_y est la somme sur les dernières périodes de (C - L_x)

       L_y est la somme sur les y dernières périodes de (H_x - L_x) avec y<x

 

 

%D est ainsi une moyenne mobile du % K (x périodes) sur les y derniers jours.

 

3.  Avantage du stochastique

 

Cet oscillateur offre l’avantage de prendre en compte les niveaux extrêmes, et non pas seulement les niveaux de clôture.

 

4.  Inconvénient du stochastique

 

L’oscillateur est souvent beaucoup trop volatil pour être utilisé directement avec le %D. Ainsi, dans la pratique, on représente souvent %D et sa moyenne mobile sur 3 périodes appelée Slow %D, qui offrent des fluctuations beaucoup plus lissées et plus utilisables.

 

 

 

Suivant la période unitaire dans laquelle ont se situe, l’importance du mouvement anticipé sera différent. En effet, plus la période unitaire sera longue, plus le mouvement anticipé sera important. Un signal de surachat sur un graphique mensuel produira un mouvement plus important que le même type de signal obtenu sur un graphique horaire.

A partir de ces notion, les analystes techniques ont développé l’indicateur de saturation.

 

D.          L’Indicateur de Saturation

 

L’indicateur de saturation peut être défini comme le niveau maximal d’une période où l’on observe un surachat ou une survente.

 

L’objectif de cet indicateur est de mesurer la force d’un surachat (survente) ou bien d’une divergence, par l’attribution d’une note. Plus le mouvement anticipé concerne une duré importante plus la note sera élevée.

 

Les analystes distinguent les signaux issus d’un surachat ou d’une survente, et ceux issus d’une divergence haussière ou baissière. Les premiers seront désignés par un chiffre, les seconds par un lettre.

 

 

Période	Surachat/survente	Divergence
5 minutes	1	A
30 minutes	2	B
1 heure	3	C
1 jour	4	D
1 semaine	5	E
1 mois	6	F

 

 

Nous avons delà vu qu’il n’existe donc plus de confusion possible à une période donnée entre la possibilité de surachat ou de survente puisqu’il s’agissait de signaux objectifs issus de modèles ondulatoires objectifs.

 

La possibilité de pouvoir noter ainsi la force de signaux objectifs est fortement utile aux utilisateur de la méthode d’Elliott, car elle permet d’effectuer un décompte correct des vagues du fait de la simplicité accrue.

 

E.          L’apport de L’Indicateur de Saturation pour la méthode d’Elliott

 

Ainsi, l’utilisation de l’Indicateur de Saturation apporte une amélioration spectaculaire dans l’appréhension de la séparation des vagues. Ainsi, la reconnaissance des formes en est fortement facilitée.

Ce problème constituait le principal obstacle à la pratique et au développement de la méthode des vagues d’Elliott.

 

Nous verrons comment chaque type de vague peut être déterminée par les signaux de surachat et survente, ainsi que par les divergences. Nous commencerons, comme nous l’avons fait dans la troisième partie, par les vagues de correction.

 

¨  La Vague 2

 

 

Au niveau de saturation considéré, dans un marché haussier, le début de la Vague 2 est marqué par un état suracheté. A la fin de la Vague 2, au même niveau de saturation, le marché est survendu (fig. 28).

 

 

Au niveau de saturation inférieur, à la fin de la Vague A, on note un marché survendu; à la fin de la Vague B, le marché est suracheté; à la fin de la Vague C, le marché est survendu et une divergence haussière peut être observée.

Cette divergence traduit un retournement de tendance au niveau supérieur, soit au niveau de référence (fig. 29).

On en déduit que le marché s’engage dans une vague d’impulsion qui est la Vague 3.

 

La même description peut être réalisée sur un marché baissier, en raisonnant dans le même sens.

 

 

figure 28

 

 

figure 29

 

¨  La Vague 4

 

A niveau de saturation considéré, le début de la Vague 4 est marqué par un état suracheté et la fin par un état de marché survendu, de même que pour la vague 2 (fig. 30). Notons qu’en principe une Vague 4 en Triangle ne verra de divergence qu’en Vague e.

 

 

figure 30

 

Au niveau de saturation inférieur, les observations réalisées précédemment restent valable pour la Vague 4 (fig. 31).

 

figure 31

 

¨  La Vague 1

 

A un niveau de saturation considéré, si la tendance principale est haussière, la Vague 1 débute par une divergence haussière.

Elle se termine sur un marché suracheté au même niveau (fig. 32).

La même observation peut être faite dans un marché baissier mais à l’inverse bien sûr.

 

Au niveau de saturation inférieur, le marché est suracheté en fin de vague (1), (3) et (5), survendu en fin de vague (2) et (4) (fig. 33).

 

¨  La Vague 3

 

Au niveau de saturation considéré, la Vague 3 débute avec des indicateurs simplement survendus (suracheté) dans le cas d’un marché haussier (baissier). Elle se termine par un état suracheté (survendu) (fig. 34)

Notons aussi qu’au niveau supérieur, on observe une inflexion de l’indicateur mais pas de sa moyenne mobile (fig. 35)

 

 

 

figure 32

 

 

 

 

figure 33

 

 

 

figure 34

 

 

 

 

figure 35

 

 

 

¨  La Vague 5

 

A un niveau de saturation donné, au départ de la Vague 5, le marché est survendu (marché haussier) (fig. 36) ou suracheté (marché baissier). Lorsque le mouvement se termine par une divergence baissière au niveau de saturation considéré, ceci signifie qu’il s’agit bien de la cinquième vague de la vague d’impulsion du niveau supérieur.

Si l’on observe plus tard que le marché présente une divergence haussière au niveau de saturation supérieur, ceci signifie que cette vague d’impulsion était la 5^ème vague qui termine la vague du degré encore supérieur.

 

 

 

figure 36

 

 

¨  La Vague A

 

 

La Vague A se termine dans un marché haussier par un état survendu, et dans un marché baissier par un état suracheté au niveau de saturation considéré fig. 37).

La sous-vague C peut se terminer par une divergence au niveau de saturation inférieur (fig. 38).

 

figure 37

 

figure 38

 

 

¨  La Vague B

 

Souvent les indicateurs fluctuent largement (fig. 37 et fig. 38). Les extrêmes précédents ne sont pas dépassés de manière à ce que les signaux indiquent simplement un surachat dans un marché haussier et une survente dans un marché baissier.

 

¨  La Vague C

 

La vague C se termine par un état suracheté si la tendance principale est baissière, et survendu si la tendance principale est haussière.

Aux niveaux de saturation inférieurs, des divergences sont observables (fig. 37 et fig. 38). Mais ces règles doivent être prises au sens de règles contingentes, comme bien souvent en analyse technique.

 

 

Ainsi, l’utilisation de l’indicateur de saturation fournit un apport considérable, car cette approche permet une décomposition des vagues d’une précision inégalée. Ceci signifie que les traders et les spielers pourront l’utiliser pour des opérations à très court terme, car l’appréhension de la durée des mouvements se fait avec une très bonne approximation. Pour repérer la fin d’une vague, il faudra que les signaux de surachat/survente indiquent un changement de tendance. Au niveau inférieur, il faudra avoir constaté une divergence peu avant. Par conséquent, pour repérer dans quelle fin de vague on se trouve, il sera nécessaire d’analyser les niveaux inférieur et supérieur au niveau de saturation considéré.

 

 

V.          Conclusion

 

Ainsi, après avoir présenté la méthode d’Elliott par ses influences, ses règles de base et les configurations rencontrées, nous avons pu présenter une tendance récente dans l’analyse technique qui est l’utilisation simultanée de plusieurs méthodes de prévision.

Cette analyse multi-méthode est un principe basé sur la réduction du risque d’erreur. Déjà, J.J. Murphy, dans Technical Analysis of the Futures Markets avait acquis la conviction qu’il existait des situations où les vagues d’Elliott sont parfaitement apparentes et d’autres où elles ne le sont pas du tout. Il est donc essentiel de pouvoir décrypter les séries de cours de manière à pouvoir y appliquer plusieurs méthodes, à plusieurs horizons temporels, afin de minimiser les erreurs. De cette manière, les signaux qui seront retenus seront ceux qui vérifient l’ensemble des modèles retenus. Un premier problème est donc le choix de ces modèles.

 

Dans notre approche, les signaux sont donnés par des modèles oscillatoires, les Stochastiques et le M.A.C.D. Ces signaux sont de type surachat/survente ou bien de type divergence haussière/baissière. Ces signaux donnent lieu à des prises de positions.

Mais l’information donnée par ces signaux doivent être analysée dans un ensemble informationnel fourni par l’application de ces modèles ainsi que du modèle des vagues d’Elliott. Cette confrontation d’informations permet de confirmer les unes par les autres. En effet, un signal sur un M.A.C.D. permettra de se préparer à un changement de direction sur les cours; se signal pourra être automatiquement confirmé ou infirmé suivant le type de vague sur lequel on se situe. A l’inverse, une figure de la méthode d’Elliott étant observée sur les cours peut être confirmée ou infirmée par les signaux et les divergences repérées sur les courbes du (ou des) modèle(s) oscillatoire(s).

 

Mais tous ces raisonnements sont effectués en prenant pour hypothèse ad hoc que les marchés sont efficients, afin de conclure que toute l’information est contenue dans le prix (i.e. le cours ). Or cette hypothèse est loin d’être vérifiée par les études réalisées dans ce domaine, ainsi que par la réalité. En effet, les comportements sur les marchés financier donnent lieu a des bulles spéculatives. Nombreux sont les auteurs qui pensent que les agents présents sur les marché financier sont irrationnels, et qui induisent par conséquent un cours plus ou moins éloigné de sa position « normale ».

Par conséquent, les cours contiendraient en plus de l’ensemble de l’information disponible certaines informations parasitant la formation des prix. Certains économistes attribuent ceci aux rumeurs et aux comportements mimétiques. De plus par l’observation des comportements micro-économiques des agents financiers, il est aisé de constater que cette attitude est assez fréquente dans les salles de marché.

 

Or, cette notion de comportements mimétiques est liée à celle d’anticipations autoréalisatrices, selon laquelle les agents qui anticipent un cours attirent le cours vers cette anticipation.

De ce fait, le succès d’une théorie telle que celle des Vagues d’Elliott ne serait elle pas due au seul fait qu’il s’agit de la théorie la plus pratiquée, et qui de plus s’autovalide en étant de plus en plus utilisée ?

 

 

 

 

 

Cassure                                                                            48

configurations                                                                  28

correction                                                                         29

degrés                                                                               22

durée                                                                                22

extension                                                                          43

Fibonacci                                                                       5; 6

Flat                                                                                  33

impulsion                                                                         39

Impulsion Standard                                                         39

Indicateur de Saturation                                                   65

l’analyse fondamentale                                                      3

M.A.C.D.                                                                        59

Nombre d’Or                                                                   10

oscillateurs                                                                       56

Poussée                                                                            35

règles de base                                                                   15

Spirale Logarithmique                                                      11

Stochastique                                                                    63

Triangle Diagonal                                                             51

Triangles                                                                          36

Zig-Zag                                                                            31