Afin d’expliciter la relation qui existe entre les risques des capitaux propres et ceux de l’actif, étant donné qu’en général le financement de l’actif se partage entre capitaux propres et dettes, il est nécessaire d’examiner les effets de l’endettement sur les risques des capitaux propres et sur la rentabilité attendue de l’entreprise.

Pour ce faire, il est important d’expliquer la relation qui existe pour une entreprise endettée, entre le risque observé de ses capitaux propres et le risque son actif.

S’il est supposé que l’entreprise est financée totalement par des capitaux propres, les actionnaires sont les seuls ayant droits à la valeur de l’actif de la firme. Le taux de rentabilité attendu de l’actif est aussi celui des actionnaires et le risque systématique de l’actif est aussi celui des capitaux propres. Or, dans une firme endettée, les créanciers interviennent aussi, et exigent de droit une partie de la valeur de l’actif.

Or, la mesure de l’impact de l’endettement nécessite un retour sur l’étude de la théorie du coût du capital, c’est à dire sur la théorie traditionnelle de l’effet de levier financier et de l’optimum d’endettement et ensuite sur la théorie de Modigliani - Miller qui prônent la neutralité de la structure du financement et la non séparabilité des décisions de financement et d’investissement.

Ainsi, l’introduction de l’endettement dans l’étude des risques des actionnaires amène une double question.

D’une part, quelle est la conséquence de l’endettement sur le risque des capitaux propres, et d’autre part quel est son effet sur la rentabilité requise par les actionnaires ?

Par conséquent, il sera intéressant de rappeler dans un premier temps les travaux classiques, d’une part de Modigliani et Miller et d’autre part du MEDAF. Puis, nous présenterons les approches synthétiques qui ont succédé, en particulier celle d’ Hamada et Rubinstein, et celle du modèle optionnel.

La recherche et la structure de financement optimale est une question complexe compte tenu de l'interdépendance entre le coût des capitaux propres et la structure de financement.

Pour comprendre la logique de la relation qui lie le coût moyen pondéré et la structure de financement, il est nécessaire de se référer à l'article de Modiglianni et Miller : coût de capital, gestion financière et théorie de l'investissement publié en 1958.

En raisonnant dans le cadre d'un marché financier parfait et en s'appuyant sur un modèle d'équilibre partiel, fondée sur la notion de classe de risque, les auteurs démontrent que la structure de financement, c'est à dire la répartition des fonds propres / dettes financières évaluée en valeurs de marché, n'avait aucune incidence sur la valeur d'une firme et par conséquent, sur le coût du capital.

L'hypothèse de perfection des marchés financiers développée par Modiglianni et Miller implique notamment que l'accès au marché financier est le même pour tout les investisseurs, que leur niveau d'information est identique et qu'il y a ni coût de transaction, ni fiscalité.

Malgré l'irréalisme de ces hypothèses, la démarche de ces deux auteurs constitue un cadre de référence car elle permet de relier clairement les décisions d'investissement et de financement de l'entreprise aux attentes des investisseurs sur le marché financier. Elle est en outre totalement cohérente avec le cadre rentabilité-risque. Le résultat obtenu repose sur l'hypothèse d'absence d'imposition des résultats.

L'introduction de l'impôt modifie très sensiblement les conclusions précédentes, car les intérêts de la dette sont déductibles ; la structure de financement influence la valeur de l'entreprise. Il devient possible d'accroître la valeur en s'endettant.

En effet, en introduisant l'impôt on en arrive à la conclusion suivante : tant que le risque de faillite n'est pas trop élevé, il est avantageux de recourir à l'endettement compte tenu de l'avantage fiscal dont il bénéficie. Cependant lorsqu'on se penche sur la structure financière on remarque qu'un endettement supplémentaire entraînait un supplément de risque financier et de risque de faillite qui pouvait compenser le gain obtenu grâce à l'économie d'impôt sur frais financiers.

Par conséquent, le recours à l'endettement doit être manié avec prudence, en tenant compte de l'accroissement du coût des fonds propres qui en résulte. Ainsi la structure de financement optimale résulte du compromis entre l'avantage fiscal et l'endettement et les coûts de faillite.

Après Modigliani et Miller, beaucoup d'auteurs se sont penchés sur ces questions. C'est ainsi que l'on a étudiée la conséquence de l'endettement sur le risque systématique (ou risque de marché) des capitaux propres et son effet sur la rentabilité requise.

L'étude du levier financier, c'est à dire des conséquences de l'endettement sur le risque et la rentabilité des fonds propres, est réalisée en partant du résultat d'exploitation ou bénéficie avant paiement des frais financiers et avant déduction de l'impôt.

De plus nous admettrons que la valeur de l'actif est considérée comme étant égale à la valeur actuelle ou valeur de capitalisation du résultat d'exploitation. Cette démarche suppose qu'une équivalence puisse être établie entre le résultat d'exploitation, assimilé au résultat économique tiré de l'actif de l'entreprise, et l'excédent de trésorerie disponible pour la rémunération des capitaux.

L'endettement de l'entreprise a pour conséquence de modifier le taux de rentabilité des capitaux propres ; nous allons définir ce taux par rapport à celui de l'entreprise non endettée.

Soit :

La valeur de l'entreprise est égale à la valeur de capitalisation du résultat d'exploitation au taux E() :

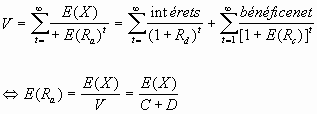
Selon cette proposition, la valeur est supposée indépendante de la structure financière de la firme.

La valeur de la firme se répartit entre créanciers et actionnaires. La valeur de la dette correspond à la capitalisation des intérêts aux taux .

Ce dernier est pris comme une donnée. Si la valeur globale est indépendante de la structure financière, la valeur des capitaux propres est égale à V-D ; elle correspond à la capitalisation, à un taux E(), du bénéfice net. le bénéfice disponible pour l'actionnaire est égal à l'espérance du résultat d'exploitation diminué du paiement des intérêts :

En conséquence,

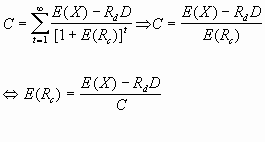
Développons cette dernière équation :

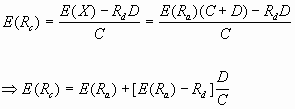
Cette équation exprime le taux de rentabilité requis par les actionnaires en fonction du taux de rentabilité économique E(), du coût de la dette et de la structure financière de l'entreprise D/C.

Si l'endettement de la firme est nul, on a avec N désignant l'entreprise non endettée :

Le taux de rentabilité des capitaux propres de l'entreprise non endettée est égal au taux de rentabilité requis pour l'actif. C'est aussi le coût du capital de l'entreprise.

Si le financement par dette est positif, le taux de rentabilité des capitaux propres augmente proportionnellement au levier financier c'est à dire proportionnellement au rapport D/C et E()est supérieur à E(). L'expression [E()-] D/C mesure l'effet de levier ou effet de l'endettement ; elle exprime le supplément de rentabilité des capitaux propres qui est requis en raison de l'existence de la dette.

Le poids du levier financier dépend du différentiel existant entre la rentabilité économique offerte par le marché et coût de la dette ; il dépend aussi de l'importance de cette dernière dans le financement de l'entreprise. Pour un différentiel de rentabilité donné, l'effet de levier est une fonction linéaire du levier d'endettement.

L'existence d'un supplément de rentabilité des capitaux propres lié à l'endettement de l'entreprise n'explique par le risque supplémentaire supporté par l'actionnaire. Ce supplément de risque est appelé risque financier. Il est compris dans le risque de marché du titre.

En effet, l'endettement influence le niveau du taux de rentabilité requis car il influence la volatilité de ce taux. A travers une application on démontre que si l'endettement est nul (D/C=0), la rentabilité des capitaux propres est celle de l'actif. Par contre, l'endettement de l'entreprise fait naître un risque pour les capitaux propres : la variabilité systématique (de marché) du taux de rentabilité est d'autant plus forte que l'endettement est élevé.

Ce surplus de volatilité, appelé risque financier de l'entreprise, vient s'ajouter au risque systématique d'exploitation de l'actif. En conséquence, le risque de marché des capitaux propres de la firme endettée se compose du risque systématique d'exploitation de l'actif et du risque financier dû à l'endettement.

Le risque financier explique que le taux de rentabilité requis des capitaux propres d'une entreprise endettée n'est pas le même que celui d'une entreprise non endettée, toutes choses égales par ailleurs.

Si la firme n’est pas endettée , l’équation relative à sa droite de marché des actifs risqués est celle de la droite de son actif. On a donc :

avec :

 : bêta de l’actif,

et :

Cette équivalence entre la rentabilité des capitaux propres et celle de l’actif s’explique en termes de risque .

Si la firme est endettée, le levier financier a pour effets :

* d'accroître la variabilité systématique du taux de rentabilité de l'actionnaire, c'est le risque financier,

* d’accroître, en raison du risque financier, le taux de rentabilité requis des capitaux propres.

Il apparaît que le bêta des capitaux propres est une fonction linéaire croissante du levier financier :

Le taux de rentabilité des capitaux propres de l'entreprise endettée

= taux sans risque

+ prime de risque d'exploitation

+ prime de risque financier

Ainsi, le taux de rentabilité des capitaux propres de la firme endettée comprend une double prime de risque : l'une pour le risque d'exploitation, ou risque de l'actif, et l'autre pour le risque financier ou risque lié à l'endettement.

L'hypothèse d'une dette sans risque et d'un bêta nul n'est acceptable que tout autant que le niveau d'endettement reste relativement faible. Au delà d'un certain niveau de dette, l'hypothèse n'est pas tenable. Cette hypothèse sera levée par la suite.

L'introduction de la dette risquée ne remet cependant pas en cause la proposition concernant le coût global du capital de l'entreprise ; cette proposition reste pertinente. En revanche, la prise en compte de la dette risquée modifie la répartition de la valeur de l'entreprise entre actionnaires et créanciers. En conséquence, elle modifie l'équation d'estimation du bêta de l'actif par rapport à celui des capitaux propres.

Ce n'est que si la dette de l'entreprise est peu ou non risquée que la formule énoncée pour évaluer le bêta de l'actif à partir de celui des capitaux propres est fiable : à cette condition, l'estimation du bêta des capitaux propres permet l'estimation du bêta de l'actif et celle du taux de rentabilité économique correspondant.

La fiscalité de l'entreprise veut qu'il existe un impôt sur le bénéfice et que cet impôt s'applique au résultat après paiement des intérêts. Il en résulte un effet automatique sur la valeur de certaines variables.

Le bénéfice disponible pour l'actionnaire est égal au résultat après intérêts et impôts. Si T est le taux d'imposition sur le revenu, on a :

Par ailleurs, l’équation représentant le revenu disponible pour la rémunération du capital devient :

avec : = revenu de l’actionnaire

et : = revenu des créanciers

Après transformation on a :

Le résultat économique après l'impôt, X(1-T), est le flux de revenu disponible pour les actionnaires si l'entreprise n'est pas endettée. Dans l'entreprise endettée, en revanche, le flux global pour la rémunération des capitaux (dettes + capitaux propres) est augmenté de l'économie fiscale réalisée en raison de l'endettement de l'entreprise.

La déductibilité des intérêts du revenu imposable augmente donc le revenu global disponible pour les investisseurs. Précisément, pour une valeur fixe de , le revenu disponible pour l'actionnaire est augmenté des économies fiscales dues à la dette.

Il résulte de ce mécanisme toute une série de conséquences liées qui vont jusqu'à influencer le coût du capital de l'entreprise.

1 - Comme le montant de flux disponible pour les investisseurs est plus élevé pour la firme endettée que pour la firme non endettée et que le taux de capitalisation est le même, la valeur de la firme endettée est plus forte :

2 - Comme l'actionnaire profite d'une économie fiscale dans la firme endettée, son taux de rentabilité attendu en tient compte. La prime de risque n'est plus calculée sur la base du différentiel entre le taux requis de l'actif et le taux sans risque. Elle est calculée en intégrant l'effet de l'accroissement de la valeur dû aux économies fiscales : elle est estimée sur la base du différentiel de la firme non endettée multiplié par (1-T). Le taux de rentabilité requis par l'actionnaire est par conséquent déterminé par l'équation :

3 - Les effets de la fiscalité affectent aussi le bêta des capitaux propres et la valeur du coût du capital engagé dans le financement d'un actif.

- Pour l’entreprise non endettée : 

- Pour l’entreprise endettée :

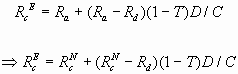
Si on remplace par sa valeur donnée par la droite de marché et ayant posé , on obtient :

Selon cette équation, la prime de risque financier par l'incidence fiscale : elle est inférieure à celle de l'entreprise équivalente non endettée avant impôt. L'explication de cette réduction de la prime de risque financier, pour raison fiscale, tient dans la baisse de la variabilité systématique de la rentabilité des capitaux propres : si les événements favorables se produisent, l'effet d'amplification à la hausse du levier financier est amoindri par la fiscalité. De même, si les événements défavorables se produisent, la fiscalité amortit le mouvement à la baisse dû au levier.

En conclusion, en réduisant la volatilité de , l'effet fiscal réduit la prime de risque financier exigible, cette réduction étant bien entendu appréciée par rapport à la prime de risque avant impôt.

4 - Le coût du capital d'un projet est fonction de sont bêta. Son estimation à partir de l'observation du bêta des capitaux propres passe par la formule d'équivalence entre les deux. C'est ce que nous pouvons établir, ayant réuni tous les éléments de son calcul pour une firme endettée et en tenant compte des effets de la fiscalité. La valeur du bêta de l'actif est égale à :

En l’absence de prise en compte de l’impôt, nous avions une valeur du bêta de l’actif donnée par l’équation :

Ainsi, l'incidence fiscale atténue l'écart entre le bêta observable des capitaux propres de la firme endettée et le bêta significatif du coût du financement total de l'entreprise correspondant au bêta de l'actif. La fiscalité a pour conséquence de faire baisser la covariation de , avec le marché et donc réduire le bêta observable pour une même valeur du bêta de l'actif.

On peut voir à travers la littérature consacrée à ce domaine qu’il est difficile de trouver une structure de financement optimale. Cependant on peut noter que l’utilisation de l’endettement est judicieuse si il est pratiqué sans excès, sachant qu’il augmente certains risques.

Nous avons vu que les propositions de Modigliani et Miller débouchent sur une définition du coût du capital qui n’intègre pas en tant que tel le niveau de risque des financements.

Aussi, il serait intéressant de s’intéresser sur la cohérence des travaux de Modigliani et Miller, au regard des enseignements fournis par le MEDAF, et de s’assurer ainsi d’une approche unifiée et synthétique du coût du capital.

L’intégration des apports du MEDAF dans l’analyse de la valeur et du coût du capital est le fait d’auteurs comme R.S. Hamada (1969) et M.E. Rubinstein (1973). Ce type d’approche donne une définition du coût du capital en fonction du risque systématique qui caractérise son affectation et en conformité avec les propositions de la neutralité de la valeur par rapport au financement de l’entreprise.

Ainsi, M.S. Hamada (1969) réalisa ses travaux sous l’hypothèse d’un coût de la dette égal aux taux sans risque, comme l’avaient déjà fait Modigliani et Miller par souci de simplification : ses résultats seront présentés dans la première partie.

Pourtant cette hypothèse n’est pas tenable ; l’entreprise ne peut accéder à un niveau d’endettement illimité sans avoir à supporter un coût supplémentaire inhérent au risque encouru par les créanciers. Par conséquent, cette hypothèse doit être remise en cause et l’analyse synthétique du coût du capital doit donc intégrer un taux de la dette fonction du risque encouru. Tel est l’objet des travaux de M.E. Rubinstein (1973), et de la seconde partie.

En partant de l’équation de mesure de la rentabilité des capitaux propres en présence d’imposition telle qu’elle est formulée par F.Modigliani et Miller, certains auteurs ont observé son comportement dans le cadre du MEDAF. La première approche dans ce sens à été fournie par M.S. Hamada (1969). Il s’agit donc ici d’observer le comportement de la rentabilité des capitaux propres dans le cas d’une dette non-risquée.

où

Cette relation exprime donc le coût des capitaux propres en fonction de la dette.

ceci avec:

Cette relation exprime le coût des capitaux propres en fonction du risque.

Dans l’analyse de Modigliani et Miller, le coût du capital de la firme N n’est pas expliquée et l’équation E(R_c^TN) º E(R_a^T) est tautologique. Le MEDAF nous apprend que ce coût est une fonction linéaire croissante du bêta de l’actif, ce dernier étant aussi le bêta des capitaux propres. Le coût du capital comme une fonction croissante du risque systémique de l’actif est a priori compatible avec l’analyse de Modigliani et Miller.

Cependant, la question qui nous intéresse est celle de l’estimation du coût du capital en fonction du risque de l’entreprise endettée. Pour l’entreprise E, on a la proposition du MEDAF qui donne le coût des fonds propres en fonction du risque, d’une part, et celle de Modigliani et Miller, d’autre part qui exprime le coût des capitaux propres en fonction de la dette.

En remplaçant Ra^T dans l’équation de Modigliani et Miller, par la valeur définie par le MEDAF, Hamada obtient :

avec  :

Le résultat obtenu par cette approche est que, dans le cas de dettes non risquées, la rentabilité requise par les actionnaires de la firme endettée est égale au taux sans risque augmenté d’une prime de risque d’exploitation et d’une prime de risque financier.

De cette relation R.S. Hamada (1969) déduit une relation entre le bêta observable et le bêta recherché pour estimer le coût du capital d’une firme endettée, la relation respectant les propositions de Modigliani et Miller, et celles du MEDAF :

Ainsi, si l’on peut et si l’on connaît le bêta des capitaux propres de l’entreprise endettés et si l’on connaît le levier d’endettement, il est possible d’estimer observer le bêta de (l’actif ou bêta des capitaux propres de la firme non-endettée), et vice versa.

Ce type d’approche a le mérite de différentier le risque d’exploitation, lié aux fluctuations du marché boursier, et le risque d’exploitation rattaché à la structure financière de l’entreprise. De plus, permet de démontrer que l’estimation du bêta de l’actif passe par celle du bêta des capitaux propres et l’observation de la structure financière de l’entreprise.

Soit :

D’autres travaux ont été effectués dans le souci de synthétiser les travaux de Modigliani Miller et le MEDAF. Tel est le cas de M.E. Rubinstein, qui lève l’hypothèse d’une dette sans risque dans l’analyse de l’impact de la dette sur le risque de l’actionnaire. En effet, on ne peut concevoir qu’un créancier prête un montant illimité sans faire supporter un coût supplémentaire lié au risque de non-remboursement. Rubinstein est un des premiers auteurs a avoir pris en compte le risque directement lié à la dette et à s’être interrogé sur ses effets.

Rubinstein suppose donc que R_d, i.e. le coût de la dette, est supérieur à R_f, i.e. le taux sans risque, et qu’il existe un b _d, i.e. un risque lié directement au prix de la dette. T.E. Conine Jr (1980) a poursuivi les travaux de Rubinstein, et a proposé, dans l’optique du MEDAF, une évaluation du taux de la dette après impôts incorporant le risque systématique de l’endettement.

Dans le cas de dettes risquées, le taux d’intérêt R_f de l’équation (1) devient R_d^T, d’où :

Intuitivement, on peut déjà sentir que, R_d^T étant supérieur à R_f, l’effet de levier sera diminué.

Conine définit la prise en compte du risque systématique de la dette comme suit :

Ainsi, en remplaçant dans (3bis), il obtient :

Donc, selon ses conclusions, le taux de rentabilité requis des capitaux propres d’une firme utilisant des dettes risquées est égal :

Par conséquent, la prise en compte du risque systématique de l’endettement a comme implication de diminuer l’effet de levier (R_a^T - R_d^T < R_a^T - R_f). Donc, il est naturel que la prime de risque financier requise par les actionnaires soit moins importante (b _c^TN - b _d^T < b _c^TN) que dans le cas de dettes non-risquées.

R_c^TE = 0,05 + 0,8 ( 0,08 - 0,05 ) + ( 0,8 - 0,4 ) ( 0,08 - 0,05 ) ´ 0,66 ´ 0,4

R_c^TE = 7,72%

La différence entre les deux taux de rentabilité exigée, dans le cas de dettes non-risquées et dans le cas des dettes risquées, provient uniquement de la différence d’un niveau de prime financier. Cette dernière est plus faible dans le cas de dettes risquées puisque l’effet de levier anticipé par les actionnaires est atténué par la croissance induite du taux d’intérêt de la dette.

Supposons maintenant que la firme augmente son endettement pour atteindre un D/CP égal à 1,2. La nouvelle rentabilité requise s’établit à R_c^TE = 7,88%. On constate donc une augmentation de la rentabilité exigée, qui est uniquement due à l’augmentation de la prime de risque financier à travers l’effet de levier.

Ainsi, nous avons pu voir qu’une approche synthétique de l’estimation du rendement espéré des capitaux propres, permet de nuancer les résultats précédemment obtenus avec les modèles classiques, sans pour autant sortir de la conclusion de la neutralité de la structure financière. En effet, l’introduction d’une dette risquée dans l’approche synthétique rend compte du phénomène en pondérant les conclusions des analyses classiques selon laquelle la valeur de l’entreprise est nettement améliorée par le recours à l’endettement. En effet, le risque systématique lié directement à la dette atténue l’effet de levier.

Une autre forme d’approche synthétique a été abordée dans la théorie financière : il s’agit d’un synthèse des résultats du modèle optionnel et du MEDAF.

La théorie des options ou Option Pricing Model (O.P.M.) est à l’origine d’une vision renouvelée du financement de l’entreprise. La description du financement de l’entreprise, en terme d’options, s’appuie sur la classification traditionnelle des sources de financement, qui oppose titres de propriétés et titres de créances.

A travers la théorie des options, l’incidence de l’endettement sur les risques des actionnaires peut être étudiée.

Ce modèle montre la nature optionnelle des positions des actionnaires et des créanciers de l’entreprise. En effet, l’émission de titres de financement (actions, obligations) d’une société peut être dépeinte en terme d’actifs optionnels sur la valeur anticipée de l’entreprise.

Les hypothèses de la modélisation, de la situation de l’actionnaire, sont les suivantes :

Il est possible d’établir le bilan prévisionnel à l’aide du modèle d’évaluation d’options de Black et Scholes datant de 1973. L’évaluation des capitaux propres repose sur des éléments exogènes, relatifs à l’entreprise considérée, qui sont la date de remboursement de la dette ou date d’exercice des options et la valeur de remboursement ou prix d’exercice, le taux sans risque.

Ensuite, elle implique l’estimation de la distribution de probabilité relative à la valeur de l’actif de l’entreprise à l’échéance de la dette.

Soient :

n : l’échéance de la dette,

_n : la valeur prévue pour le remboursement de la dette,

_n : les valeurs prévisionnelles de la valeur de l’actif,

_n : les valeurs anticipées des capitaux propres.

La valeur des capitaux propres est donnée par la différence entre la valeur de l’actif et le remboursement de la dette.

Avec le bilan prévisionnel et le modèle d’évaluation des options, il est possible d’estimer la valeur des capitaux propres et la valeur actuelle de la dette ;

Soient :

V₀ : la valeur actuelle de l’actif,

C₀ : la valeur actuelle des capitaux propres qui est égale à la valeur de l’option d’achat sur la valeur de l’actif,

P₀ : la valeur de l’option de vente qui correspond à la prime de risque de la dette,

₀ : la valeur actuelle de la dette au taux sans risque,

R_F : le taux sans risque,

R_i : le taux de la dette risquée.

Le bilan financier de l’entreprise peut être représenté par l’équation suivante :

Valeur de l’option d’achat sur l’actif de l’entreprise

+ Valeur actuelle de la dette au taux sans risque

= Valeur de l’actif de l’entreprise

+ Valeur de l’option de vente sur l’actif de la société

La valeur de l’option d’achat correspond à celle des capitaux propres. La valeur du put représente la prime de risque défaillance de l’entreprise qui peut être demandée par les créanciers contribuant au financement de l’entreprise.

La valeur de la dette sans risque, moins la valeur de l’option de vente, donne la valeur d’une dette risquée. Il est par conséquent possible de poser une nouvelle équation du bilan financier de l’entreprise :

Valeur des capitaux propres

+ Valeur de la dette risquée

= Valeur de l’actif de l’entreprise

Si la valeur de l’option de vente, dépendant de son prix d’exercice pour des valeurs prévisionnelles de l’actif, tend vers zéro, la valeur de la dette tend vers la dette non risquée.

Ceci n’est vrai que si ce sont les actionnaires qui assument la totalité du risque systématique d’exploitation de l’entreprise, les créanciers prêtant au taux sans risque.

Les actionnaires semblent endosser, ici, le risque systématique du titre. En fait, en achetant une option de vente, les actionnaires achètent le droit de n’être responsables à l’égard des créanciers qu’à concurrence de leur apports en capitaux propres.

Une positon optionnelle n’implique pas l’existence proprement dite de l’option correspondante, il est possible qu’elle découle d’une combinaison d’opérations relatives, soit, à des actifs conditionnels, call ou put, soit, à l’actif sous jacent, ou encore à des opérations de prêt ou d’emprunt à un taux sans risque.

Les positions optionnelles des actionnaires, comme celles des créanciers, sont, en conséquence, les résultantes de combinaison (prêt et emprunt au taux sans risque, achat et vente d’options).

il est possible de rapprocher les deux visions en terme d’option de vente et d’achat pour avoir une représentation optionnelle du financement de l’entreprise.

Tout se passe comme si l’actionnaire, décidait de vendre l’actif aux créanciers pour un montant équivalent à la valeur actuelle de la dette et achetait simultanément une option d’achat sur l’actif cédé.

Considérons une entreprise E endettée et son bilan financier prévisionnel en valeur de marché à l’échéance d’un an. Sa valeur d’actif prévisionnelle est donnée par une distribution de probabilité dont l’espérance est V₁ . Et, V_o, la valeur actualisée de marché de l’entreprise, en t = 0.

Considérons une option d’achat négociable à un an sur les actions de la société E, dont le prix est C. Ce titre donne à son détenteur le droit d’acheter les actions de la société E dans un an, au prix d’exercice PE.

L’entreprise E se finance par de la dette pour un montant égal à D_o , la dette est à échéance d’un an, et, sa valeur de remboursement prévue est de D₁ .

Si la valeur de l’actif est supérieure à la valeur de remboursement de la dette D₁, les actionnaires bénéficient de la valeur résiduelle V₁ - D₁ . L’actionnaire se positionne comme acheteur d’une option d’achat sur la valeur de l’actif.

Si la valeur de l’actif est inférieure à D₁ , la valeur des capitaux propres est nulle. L’actionnaire va abandonner la valeur de l’actif aux créanciers qui seront remboursés à concurrence de la valeur de l’actif. Dans ce cas, tout se passe comme si les actionnaires étaient détenteurs d’une option de vente à l’égard des créanciers. Voir ci-dessous :

En effet, l’actionnaire qui resterait détenteur de l’actif, ferait l’emprunt du capital auprès des créanciers au taux sans risque, et, achèterait auprès des créanciers une option de vente sur l’actif ayant pour prix et date d’exercice la valeur et la date de remboursement de la dette.

En résumé, le profil du gain de l’actionnaire, de la firme endettée, est celui observable pour toute option d’achat sur titre, de même prix et même date d’exercice que ceux de la dette. Il est négatif et égal au montant initial investi C₀ par l’actionnaire, si le montant de l’actif est inférieur à la valeur de la dette.

A la suite, il augmente avec V₁, et, est égal à ( V₁- D₁) - C₀ pour toute valeur de V₁ supérieure à D₁. Cf. figure 1

Figure 1 : Profil de gain de l’actionnaire de l’entreprise endettée.

A l’échéance, l’actionnaire, détenteur de l’option d’achat, réalise l’une des deux alternatives offerte par l’option :

Si la valeur de l’actif est inférieure au prix de rachat prévu, ou prix d’exercice, l’actionnaire abandonne l’option ;

Si la valeur de l’actif réalisée est, en revanche, supérieure au remboursement de la dette, l’actionnaire exerce son option et rachète la valeur de l’actif au prix convenu.

Dans ce cas, les actionnaires paraissent couverts si la valeur de l’actif évolue défavorablement.

Ainsi, la richesse de l’actionnaire à l’échéance de la dette est compris entre 0 et V₁-D₁ en fonction de la valeur de l’actif à l’échéance :

Ce résultat peut s’appliquer sur n périodes.

Pour conclure, le financement de l’entreprise peur se décrire de la façon suivante :

Les capitaux propres de l’entreprise endettée peuvent être considérés comme une option d’achat sur la valeur de l’entreprise. Le prix et la date d’exercice de l’option correspondent respectivement à la valeur et à la date de remboursement de la dette.

Les créanciers sont vendeurs auprès des actionnaires d’une option de vente sur la valeur de l’actif de l’entreprise. Ce put possède les mêmes prix et dates d’exercice que l’option d’achat. L’option de vente est équivalente à la valeur de la responsabilité limitée des actionnaires par rapport aux créanciers, c’est à dire à la prime de risque de la dette. Si le put a une valeur positive ( il existe un risque de défaillance), la dette est une dette risquée.

Il convient, à présent, d’étudier l’évaluation des taux de rentabilité des capitaux propres et de la dette selon le modèle optionnel et en fonction de leur risque systématique respectif. Le risque global étant fonction du risque systématique de l’actif et de la structure financière.

Cette analyse semble nécessaire pour effectuer l’étude de l’impact de la dette sur les risques supportés par les actionnaires et de qui plus est, sur leur taux de rentabilité requis.

L’analyse de la valeur et du coût du capital d’après le modèle d’évaluation d’option repose sur un certain nombre d’hypothèses importantes.

L’approche qui a combiné les deux analyses de l’OPM et du MEDAF est celle de Hsia (1981). Son approche algébrique a démontré la convergence et la cohérence des analyses de la valeur et du coût du capital.

Tout d’abord, l’OPM implique que les transactions, relatives aux options, se déroulent en temps continu.

De plus, il suppose que les agents ont les mêmes anticipations sur le processus aléatoire décrivant la valeur de l’actif sous jacent. Et enfin, selon l’OPM, la valeur de l’option est complètement dérivée du processus de prix du sous jacent, il est supposé décrire toute l’incertitude pertinente du marché.

A partir de cette dernière hypothèse, l’évaluation par l’OPM, des capitaux propres et de la dette, induit l’indépendance de la valeur de l’entreprise vis à vis de son financement. Par conséquent, le modèle des options considère valides les propositions de Modigliani-Miller.

L’hypothèse de continuité du modèle OPM nous amène à utiliser une version en continu du MEDAF, proposé par R.C.Merton. Dans son analyse, il apparaît qu’il n’y a aucune différence entre le modèle traditionnel, à une seule période, et sa version en temps continu.

Afin d’établir l’expression du risque systématique selon le modèle des options, il est nécessaire, dans un premier temps, de poser l’équation de la droite de marché des actifs risqués selon le modèle en continu de Merton. Cette droite est, néanmoins, identique à celle de Sharpe-Lintner.

Et enfin, L’hypothèse des anticipations, communes à tous les agents, reste la même pour le MEDAF.

Soient :

E(R_i) : taux de rentabilité instantané attendu pour l’actif risqué i,

b _i : Risque systématique instantané de l’actif i,

b _i  = Cov ( R_i, R_m)  / var(R_m)

E(R_m) : Taux de rentabilité instantané attendu pour le portefeuille de marché,

R_F : Taux d’intérêt sans risque, taux non aléatoire.

Pour réunir les deux modèles, il est plus simple de partir de l’équation différentielle stochastique de Black et Scholes.

Soient : C : le cours des capitaux propres de l’entreprise, ou cours de l’option d’achat,

V : la valeur de l’entreprise endettée, V le sous jacent de l’option,

s ² : la variance instantané de la valeur de l’entreprise,

t : Le temps,

Le changement du prix du titre est lié au changement de la valeur de la firme.

En divisant par C, il est possible d’obtenir :

Les rapports et sont respectivement le taux de rentabilité des capitaux propres, R_c, et le taux de rentabilité économique de l’entreprise, R_a. Et, , représente la part relative des capitaux propres dans la valeur de l’entreprise.

Par conséquent, la relation entre la rentabilité des capitaux propres d’une entreprise endettée et sa rentabilité économique sont :

A présent, soient, b _i et b _a, respectivement, le risque systématique instantané des capitaux propres de la firme endettée et le risque systématique de l’actif. Par définition,

Il devient, donc, possible d’exprimer le risque systématique de capitaux propres de l’entreprise endettée en fonction du bêta de l’actif, de la structure financière et de la variation de capitaux propres par rapport à la variation de la valeur de l’actif :

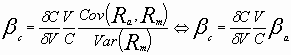
Dans le modèle optionnel, la valeur des capitaux propres de l’entreprise est représenté par l’équation suivante :

où, E : valeur de remboursement de la dette ou prix d’exercice du call,

R_F : le taux sans risque,

T : la durée jusqu’à l’échéance de la dette.

N(.) : probabilité qu’une variable normale centrée réduite soit inférieure ou égale à la valeur d.

et,

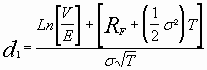
La dérivée de la valeur des capitaux propres par rapport à la valeur de l’actif sous jacent est :

En substituant, cette valeur dans l’équation du bêta des capitaux propres de la firme endettée :

Des lors, il est possible d’établir une relation entre le bêta des capitaux propres de la firme endettée et le bêta de l’actif ou bêta de l’entreprise non endettée, et, d’observer l’influence de l’endettement sur le risque des actionnaires détenteurs des capitaux propres.

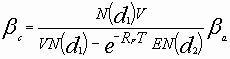
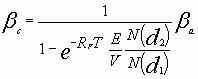
Comme E / V £ 1, < 1, et , le résultat est b _{c ³} b _a > 0.

Alors, le risque systématique des capitaux propres de la firme endettée est plus important que le risque systématique d’une firme non endettée. A noter que le bêta des capitaux propres de l’entreprise endettée est une fonction monotone du taux de l’endettement. Dans cette situation, l’endettement a un impact sur le risque de l’actionnaire, puisqu’il entraîne nécessairement une augmentation du risque.

Cette équation, grâce au modèle de Black et Scholes, permet d’analyser le risque systématique de l’action de la firme endettée en fonction de tous les déterminants de la valeur d’un call. Il va, par conséquent, en résulter des propositions sur les éléments qui ont une action sur le risque systématique des capitaux propres.

Au niveau des actionnaires, principalement, le risque systématique des capitaux propres augmente si la valeur de remboursement de la dette augmente et inversement. C’est la même relation qui a été mise en évidence dans l’analyse du levier financier.

De plus, après avoir explicité les relations entre les bêta des capitaux propres et de la dette, il convient de définir, à présent, le taux de rentabilité relatif au capitaux propres pour voir l’influence de la dette.

La rentabilité des capitaux propres en fonction du risque d’activité et du levier financier peut s’exprimer à partir de l’équation de la droite d’un actif risqué et de l’expression du risque des capitaux propres selon l’OPM.

Pour une firme non endettée, il y a ;

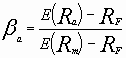
L’équation du taux de rentabilité des capitaux propres de l’entreprise endettée est donnée par :

Le taux de rentabilité requis des capitaux propres est égal au taux sans risque augmenté d’une prime risque . La prime de risque est une fonction croissante de la structure du financement de la firme. Le risque des actionnaires est, par conséquent, influencé par l’endettement, et, semble être augmenté d’une prime de risque supplémentaire, provoquée par l’effet de levier financier. Il semble, donc, raisonnable de conclure à l’incidence de l’endettement sur les risques supportés par les actionnaires.

Le champ théorique, utilisée, pour établir l’incidence du risque d’endettement sur les risques des actionnaires, repose sur la base de la théorie financière de l’entreprise et des marchés. En effet, le cadre de référence proposée par Modigliani-Miller, le MEDAF, et l’OPM de Black et Scholes semble s’unifier et ainsi, renforcer la validité de leurs hypothèses.

Différentes études empiriques ont été réalisées dans le but de rechercher les effets de l’endettement sur l’entreprise. La première a été effectuée en 1970, par Beaver, Kettler et, Scholes où il a été montré que plus l’endettement était important, plus le risque de la société concernée est élevé, donc l’endettement devrait être positivement corrélé avec le risque systématique.

En 1972, Hamada a montré que sur le marché américain, le taux d’endettement explique en moyenne 21% à 24% de la valeur du bêta.

En 1976, Jacquillat, Levasseur, et Pène ont obtenu un résultat similaire dans une étude où les ratios d’endettement qui suivent, étaient aussi positivement corrélés avec le bêta ; Frais financiers / bénéfices net, dettes totales / passif total, dettes long terme /( dettes long terme + fonds propres).

Par conséquent, les tests empiriques semblent confirmer le fait que l’endettement augmente les risques des actionnaires.

Naturellement, ces conclusions s’inscrivent dans le cadre de la théorie financière pure, abstraction faite des apports de la théorie de l’agence et de la théorie de signaux.

Bibliographie

BLACK F. AND SCHOLES M., « The princing of options and corporate liabilities », Journal of political economy, vol 81, n°3, 1973, p. 637-659.

CHARREAUX G., « Gestion financière », Litec, 1991

CONINE T.E. Jr, « Debt capacity and the capital budgeting decision : a comment », Financial Management, Vol 9/1, printemps 1980, pp. 20-22.

COPELAND T.E.,WESTON J.F., « Financial theory and corporate policy », Addison Wesley, third edition, 1988.

HAMADA R.S., « Portfolio Analysis, Market Equilibrium, and Corporation Finance », Journal of Finance, mars 1969

MATHE J.C., A. RIVET, « Effet de levier et risque d’endettement : essai de synthèse et prolongement », Banque & Marchés, n° 14, juillet-août 1994

MERTON R.C., « An intertemporal Capital Asset Pricing Model », Econometrica, Septembre 1973.

MODIGLIANI F., M.H. MILLER, « The cost of capital, corporation finance, and the théory of investment », American Economic Review, juin 1958

MODIGLIANI F., M.H. MILLER, « Corporate income taxe and the cost of capital», American Economic Review, juin 1963

MOURGUES N., « Financement et coût du capital de l’entreprise », Economica, 1993, Paris.

RUBINSTEIN M.E., « A Mean-Variance Synthesis of Corporate Financial Theory », Journal of Finance, mars 1973